Adversarial Search

Adversarial Games §

• Adversarial games are everywhere, i.e. Tic Tac Toe, Checkers, Chess etc
• Many different kinds of games
• Axes:
  • Deterministic vs Stochastic
  • One, two or more players
  • Zero sum vs General sum
  • Perfect information (can you see the state) vs Partial information
• Algorithms need to calculate a strategy (policy) which recommends a move (action) from each position (state)
  • This differs from previous Search Problems

Deterministic Games §

Problem Formulation

• States: $S$ (start at $S_0$)
• Players: $P=\{1\dots N\}$ (take turns)
• ToMove(s): the player whose turn it is to move in state $s$
• Actions(s): the set of legal moves in state $s$
• Result(s, a): the Transition function, state resulting from taking action $a$ in state $s$
• IsTerminal(s): a terminal test, true when the game is over
• Utility(s, p): $S\times P$ -> a number: final numeric value to player $p$ when the game ends in state $s$ Solution for a player is a policy which maps a state S to an action A

Zero-Sum Games §

• Agents have opposite utilities (values on outcomes)
  • If player 1 does something positive, its negative for player 2
• Can then think of outcome as a single value that one maximizes, and the other minimizes
• Adversarial, pure competition

General Games §

• Agents have independent utilities
• Cooperation, indifference, competition, and more are all possible

Optimal Decisions in Games §

Adversarial Search §

• Single Agent Trees
  • For each state we figure out the best achievable outcome (utility) from that state
    • For terminal states that value is known
    • Non-terminal states:
      • $V(s)={\text{max}}_{s^{\prime }\in \text{children(s)}}V(s^{\prime })$
• Adversarial Game Trees
  • We use a similar concept, but now we can include the opponents moves after our move to see the best states and choose the best path
  • 
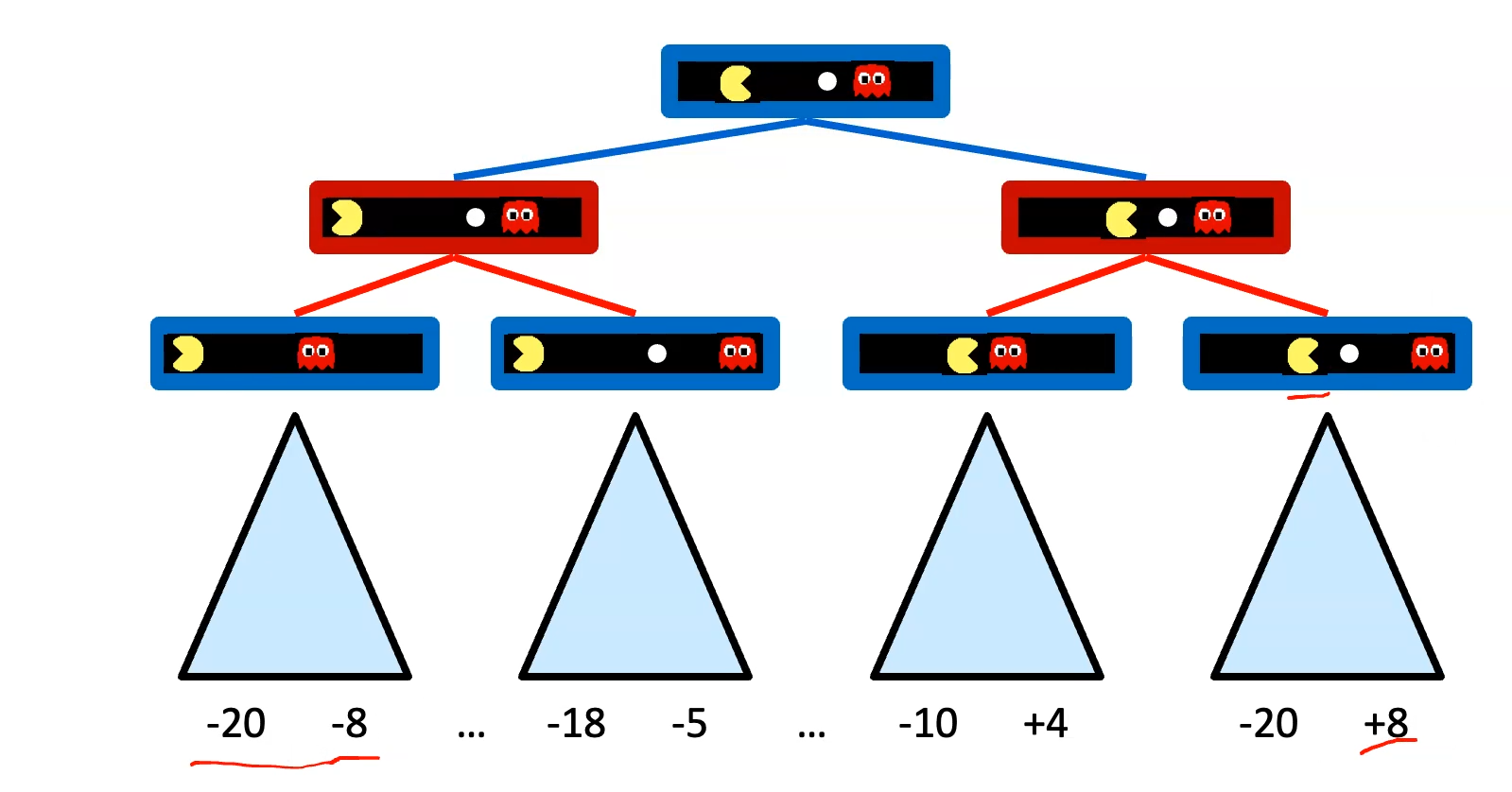
• Minimax Search
  • Use in Deterministic, Zero-sum games:
    • Tic tac toe, chess, checkers
    • One player maximizes result
    • The other minimizes result
  • A state-space search tree
  • Players alternate turns
  • Compute teach nodes minimax value: the best achievable utility against a rational (optimal) adversary
• Implementation

def max-value(state):
	initialize v = -infinity
	for each successor of state:
		v = max(v, min-value(successor))
	return v

def min-value(state):
	initialize v = +infinity
	for each successor of state:
		v = min(v, max-value(successor))
	return v

The two functions just keep calling each other recursively

def value(state):
	if the state is a terminal state return the states utility
	if the states agent is MAX return max-value(state)
	if the states agent is MIN return min-value(state)

Minimax is optimal against a RATIONAL player. If they aren’t being rational and choosing randomly then it might not be optimal to keep using the min max.

• Minimax Efficiency
  • Just like exhaustive DFS
  • Time $O(b^m)$
  • Space $O(bm)$
• So the real question is, is it necessary to explore the entire tree? Can we cut things to reduce the amount of time we are searching?

Alpha Beta Pruning §

• We can sometimes prune paths from the tree to go faster
• General configuration (MIN version)
  • When computing the MIN-VALUE at some node $n$
  • We loop over $n$’s children
  • $n$’s estimate of the children’s min is dropping
  • Who cares about $n$’s values? MAX
  • Let $\alpha$ be the best value that MAX can get at any choice point along the current path from the root so far
  • If $n$ becomes worse than $\alpha$, MAX will avoid it, so we can stop considering $n$’s other children
• MAX version is symmetric, just flip MIN to MAX, change alpha to beta, and, worse to better etc
• Combine the two you get alpha beta pruning
• Implementation

alpha: Max's best option on path to root
beta: Min's best option on path to root

def max-value(state, alpha, beta):
	initialize v = -infinity
	for each successor of state:
		v = max(v, value(successor, alpha, beta))
		if v >= beta return v
		alpha = max(alpha, v)
	return v
	
def min-value(state, alpha, beta):
	initialize v = +infinity
	for each successor of state:
		v = min(v, value(successor, alpha, beta))
		if v <= alpha return v
		alpha = min(beta, v)
	return v

Properties

• This pruning has no effect on the minimax value computed for the root

• However, the values of the intermediate nodes might be wrong

  • Important: children of the root may have the wrong value
  • So, the most naïve version won’t let you do action selection
  • Need to keep track which nodes have been pruned

• Good child ordering improves effectiveness of pruning

• With “perfect ordering”

  • Time complexity drops to $O(b^{\frac{m}{2}})$
  • Doubles solvable depth

• In most realistic games you cannot search to the leaves

• So instead we can check to a certain depth

• Depth-limited search

  • Instead, search only to a limited depth in the tree
  • Replace terminal utilities with an evaluation function for non-terminal positions
  • Guarantee of optimal play is gone; more depth makes a big difference

Heuristic Alpha Beta Pruning §

• Use Evaluation functions!
• Treat nonterminal nodes as if they were terminal
• Eval(s): Evaluation function
• IsCutOff(s) a cutoff test, true when we stop searching
• What should we use for the evaluation functions?
  • Desirable properties
    • Order terminal states in same way as true utility function
    • Strongly correlated with the actual minimax value of the states
    • Efficient to calculate
  • Typically us features - simple characteristics of the game state that are correlated with the probability of winning
  • The evaluation function combines feature values to produce a score
• Evaluation functions are always imperfect
• The deeper in the tree the evaluation function is buried, the less the quality of the evaluation function matters
• An important example of the tradeoff between complexity of features and complexity of computation

Monte Carlo Tree Search (MCTS) §

• Instead of using a heuristic evaluation function, can we esitimate the value by averaging utility over several simulations
• Smimulation (also called playout or rollout) chooses moves first for oen player, then the other, repeeating until a termianl position is reached
  • Choose moves either randomly or according to some playout policy (choose good moves)
• Exploration (try nodes with few playouts) vs exploitation (try nodes that have done well in the past)

Stochastic Games §

What if a game has a “chance element”?

• Our game tree gets much larger
• The sum of the probability of each possible outcome multiplied by its value:$E(X)=\sum _i{p}_i{x}_i$
• Now three different cases to evaluate, rather than just two
  • MAX, MIN, CHANCE
• EXPECTED-MINIMAX-VALUE(n) =
  • Utility(n) if terminal node
  • max expected-minimaxvalue if its a max node
  • min expected minimax value if min node
  • P(S) times expected minimax value for every successor summed if a chance node