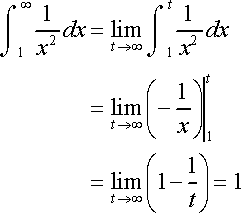Convergence means the series or sequence or integral eventually approaches a finite number.
Divergence means the series or sequence or integral never approaches a finite number, it just continues to grow.
In Sequences
A Sequence converges if its terms approach a finite number. What a sequence converges to (if anything) can be found by doing the limit (some number) where is the explicit form of the sequence. For the series to converge, the limit has to equal some number. This number is known as the Limit of the Sequence.
A Sequence diverges if the limit . This means the terms of the sequence never approach a finite number.
Example
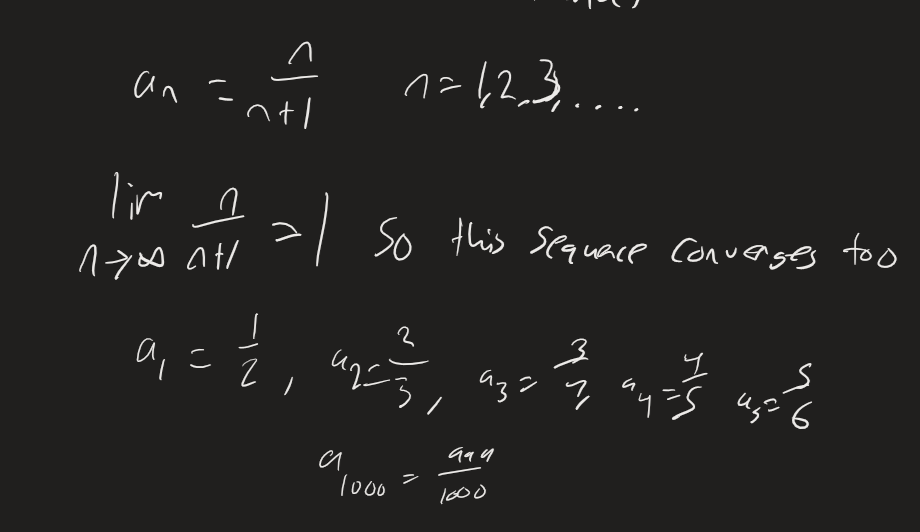
In Series
A Series converges if it eventually reaches a finite sum. Another way of putting it is if the Sequence of the partial sums converges, then the series converges.
The limit as n approaches infinity of exists. This means no matter how many terms are added , the sum will never exceed 1 (the result of the limit above). Thus the series converges to 1.
Absolute/Conditional Convergence
A series that is absolutely convergent is also convergent. If a series converges, but not absolutely, then it is conditionally convergent. Absolutely convergent means that the series converges when the absolute value of its terms are taken.
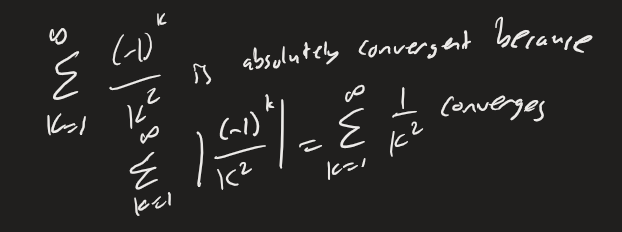
Why does absolute convergence imply convergence?
We know If you add to all parts you end up with If you sum those for all k you get the following, This means that if converges, then the series is trapped between 0 (a finite number) and another finite number and therefore also must converge.
A series that is conditionally convergent sums up to a different number if you rearrange the terms in the series. An absolutely convergent series will always add up to the same sum.
In Improper Integrals
If the improper integral has a finite answer, it is convergent. Otherwise it is divergent.