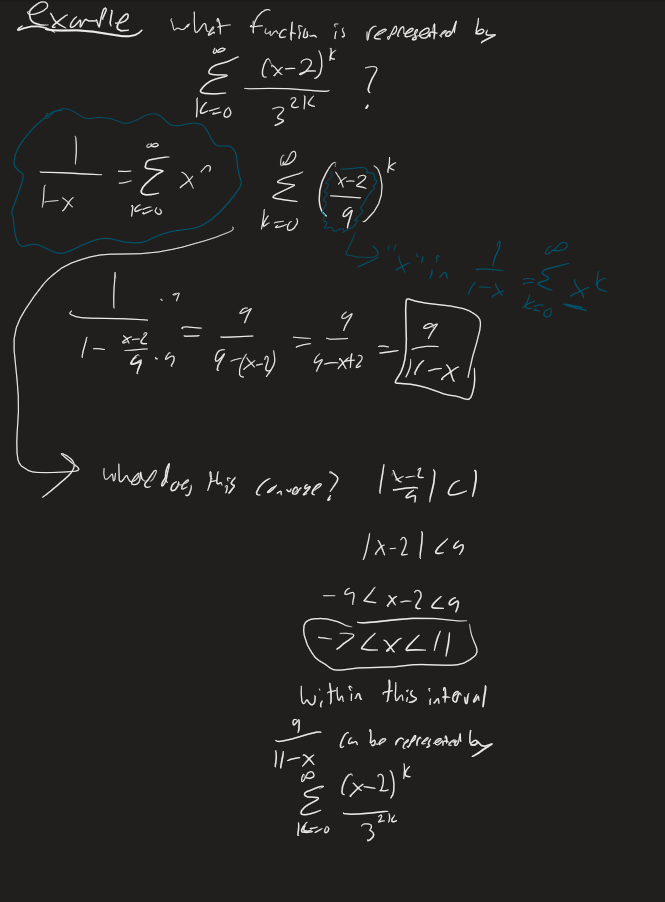Power Series

#Calc-2#Math#Series A Power Series is a type of Series where you write a function, f(x) as a series which ends up being a polynomial of very high degree.

Power Series are often of the form $\sum _{k=0}^{\infty }{C}_k(x-a{)}^k=C_0+C_1(x-a)+C_2(x-a{)}^2+C_3(x-a{)}^3+...$ $a$ is called the center of the power series $C_k$ is the coefficient of the kth degree term

Any series where $x$ is in the $a_k$ can be considered a power series

A very often used power series is called the Taylor Series

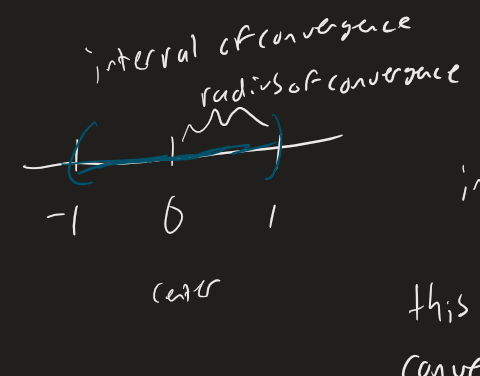
Convergence of Power Series §

The convergence of a power series often depends on x

For example, the geometric series $\sum _{k=0}^{\infty }{x}^n=1+x+x^2+x^3+...$ converges if $|x|<1$. This means it converges on the interval (-1 < x < 1) or from (-1, 1) in interval notation

The series is said to have a radius of convergence of 1.

Example §

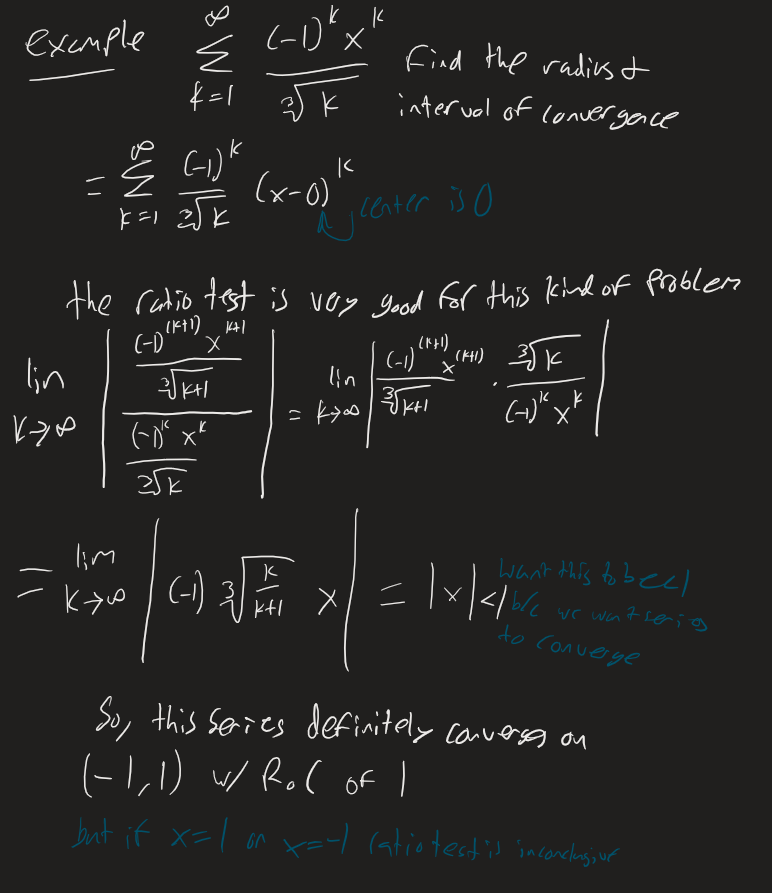
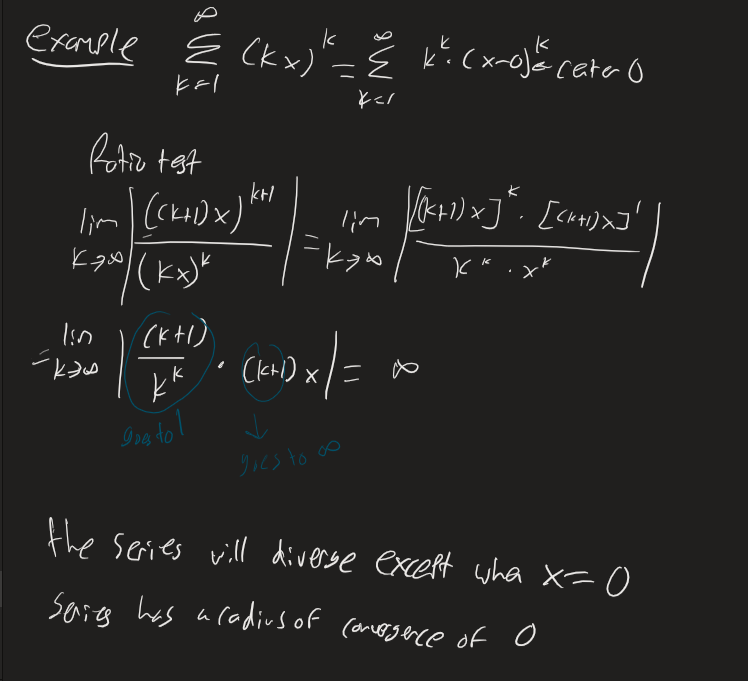
Writing Functions as Power Series §

We know that $\sum _{k=0}^{\infty }a{r}^k=a+ar+a{r}^2+a{r}^3+...=\frac{a}{1-r}$ so long as $|r|<1$

Now if we let $a=1,r=x$ then $\frac{a}{1-r}=\frac{1}{1-x}=\sum _{k=0}^{\infty }{x}^k=1+x+x^2+x^3+...$ for $|x|<1$. This is the same as the Taylor Series of $f(x)=\frac{1}{1-x}$ with $a=0$

We can modify this series to find the power series of a similar function.

Convert the function into a form similar to $\frac{1}{1-x}$ and replace x in the power series with whatever new x you get from converting the function.

$\frac{1}{1+x}=\frac{1}{1-(-x)}=\sum _{k=0}^{\infty }(-x{)}^k=1-x+x^2-x^3+x^4-...,|x|<1$

The “1” in the denominator of $\sum _{k=0}^{\infty }{x}^k=\frac{1}{1-x}$ is very important. If it gets replaced by another number you have to adjust to change it back into a 1.

Differentiation and Integration §

We can differentiate and integrate known power series to find power series of similar functions.

For example, lets use $f(x)=\sum _{k=0}^{\infty }{x}^k=\frac{1}{1-x},|x|<1$ to find the power series of $g(x)=\frac{1}{(1+x^2{)}^2}$

We can find the power series of $\frac{1}{1+x^2}$ but how do we get the second square?$\frac{d}{dx}\left(\frac{1}{1+x^2}\right)=\frac{-2x}{(1+x^2{)}^2}=-2x\ast g(x)$ this means that $g(x)=\frac{-1}{2x}\ast \frac{d}{dx}(\frac{1}{1+x^2})$ We can sub in the power series of $1/1+x^2$ and differentiate its terms

$g(x)=\frac{-1}{2x}\ast \frac{d}{dx}(\sum _{k=0}^{\infty }(-1{)}^k{x}^{2k})$ $=\frac{-1}{2x}\ast \frac{d}{dx}(1-x^2+x^4-x^6+x^8-...$ $=\frac{-1}{2x}\text{*}(-2x+4x^3-6x^5+8x^7-10x^9+12x^{11}-...)$ $=1-2x^2+3x^4-4x^6+5x^8-6x^{10}$ We have to write the above as a summation to get the final series. To write it as a summation, look at the patterns in the terms. Patterns: Alternating signs, starting at k = 1, k is the coefficient of each term. The power of each x is 2k-2 Final Power Series: $\sum _{k=1}^{\infty }(-1{)}^{k+1}k{x}^{2k-2}$ If we choose or are told to start at a different k, then the series will be different

Note: Differentiation and Integration DO NOT affect the radius of convergence of the parent series Here, we differentiate $\frac{1}{1+x^2}$ which converges for $|-x^2|<1$ , which means that our new series also converges for the same values. The endpoint behavior may however change.

Example - Integration §

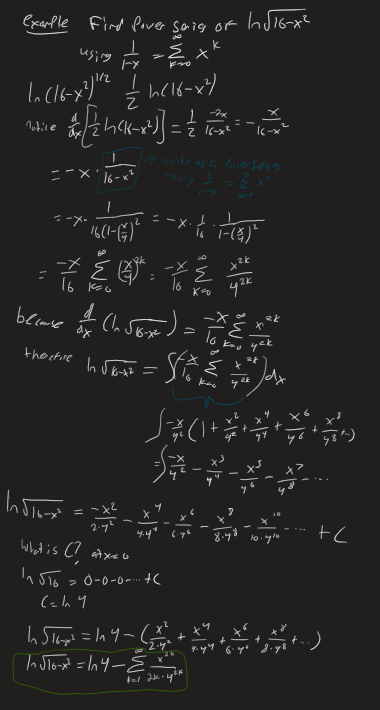
Example converting a Power series to a function §