Sorting

#Sorting#Computer-Science#CS251 A sorted array looks like this $\text{A}=[a_0,a_1,a_2,...,a_{n-1}]$ Such that $a_i\le a_{i+1}$

Any sorting algorithm solves the following problem. “Given an unsorted array, decide how to permute the array such that the array elements are sorted”

• Sorting is a decision making algorithm, the algorithm has to choose things.

There are 4 main things we look at in sorting algorithms

Stability §

• Does it keep it’s output stable?
• This may or may not be important based on the problem
• Example: $\text{A}=[2_0,2_1,0]$
• If sorting algorithm returns $[0,2_0,2_1]$ it is stable. The ordering of like elements is preserved.
• If it returns $[0,2_1,2_0]$ it is considered unstable

Certification §

• Can we prove the algorithm will work?
• This can be trivial or it can be difficult

Runtime Complexity §

• How fast is it?
• We analyze this with Runtime Expressions and Big O Notation

Space Complexity §

• If a copy of the array is needed, the algorithm will require more space
• An In Place algorithm works directly on the input array
• A not in place algorithm needs some copy of the input to work

Lowest Runtime Proof §

No sorting algorithm can do better than $O(n\log n)$ with compares/swaps.

Let’s consider an array of 3 elements. $[a_1,a_2,a_3]$ Let’s make a decision tree of every comparison a sorting algorithm COULD do on this array.

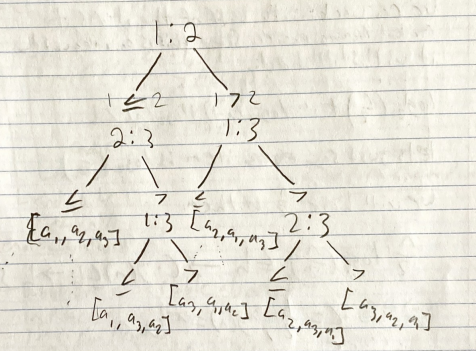
The leaves of this tree correspond to every permutation of the array. We have n! leaves, sorting algorithms find one of the n! permutations that is sorted.

This isn’t a full binary tree, it’s missing 4 leaves (shown with dotted lines). $n!\le 2^h$ $\text{the \# of permutations of n items}\le \text{the \# of leaves possible for this tree}$ $n!\le 2^h$ ${\log }_2|n!|\le h$ ${\log }_2(1\cdot 2\cdot 3\cdot ......\cdot n-1\cdot n)\le h$ ${\log }_2(1)+{\log }_2(2)+....+{\log }_2(n)\le h$ We can work with half of the items to make proving easier. Since this is an inequality, it will still hold. ${\log }_2(\frac{n}{2})+....+{\log }_2(n-1)+{\log }_2(n)\le h$ Let’s just say every item is ${\log }_2(\frac{n}{2})$ We will have $\frac{n}{2}$ of them

$\frac{n}{2}{\log }_2(\frac{n}{2})\le h$ $C\cdot g(n)\le h\cdot \to h\in \Omega (n{\log }_2(n))$ $C=\frac{1}{2},g(n)=n{\log }_2(n))$

A sorting algorithms number of compares CANNOT grow slower than $n\log n$ We can only do faster sorting if we don’t compare items. This leads to the use of Non-Comparison Sorts

Sorting Algorithms §

There are various sorting algorithms. Here’s basic information on each, go to each sorting algorithms individual page to see more about it.

Bubble Sort §

• Best Case $O(n)$
• Worst Case $O(n^2)$
• Stable
• In Place

Selection Sort §

• Best Case $O(n^2)$
• Worst Case $O(n^2)$
• NOT Stable
• In Place

Insertion Sort §

• Best Case $O(n)$
• Worst Case $O(n^2)$
• Stable
• In Place
• Variation: Shell Sort

Heap Sort §

• $\Theta (n\log n)$
• Not Stable
• In Place

Merge Sort §

• $\Theta (n\log n)$
• Stable
• Not In Place

Quick Sort §

• Best Case $O(n\log n$)
• Worst Case $O(n^2)$
• Not Stable
• In Place

Counting Sort §

• $O(n+k)$
• Stable
• Not in Place

Radix Sort §

• Time depends on sorting algorithm used
• Stable
• Not in place