Ratio Test

#Calc-2#Math#Series Given $\sum _{k=1}^{\infty }{a}_k$ the series will converge absolutely (and therefore converge) if $li{m}_{k\to \infty }|\frac{a_{k+1}}{a_k}|<1$ The series diverges if $li{m}_{k\to \infty }|\frac{a_{k+1}}{a_k}|>1$ The test is inconclusive if $li{m}_{k\to \infty }|\frac{a_{k+1}}{a_k}|=1$

Why? If $li{m}_{k\to \infty }|\frac{a_{k+1}}{a_k}|=r$ , then this means that as k becomes large, $|a_{k+1}|\approx r|a_k|$ which means that each term is r times the previous one, behaving like a geometric series. And a geometric series converges for |r| < 1

The process §

replace all the k’s in the original $a_k$ with (k+1) and divide it by the original. Take the limit as k approaches infinity and the absolute value. Often you will end up multiplying by the reciprocal of the bottom and doing a lot of canceling out

Examples §

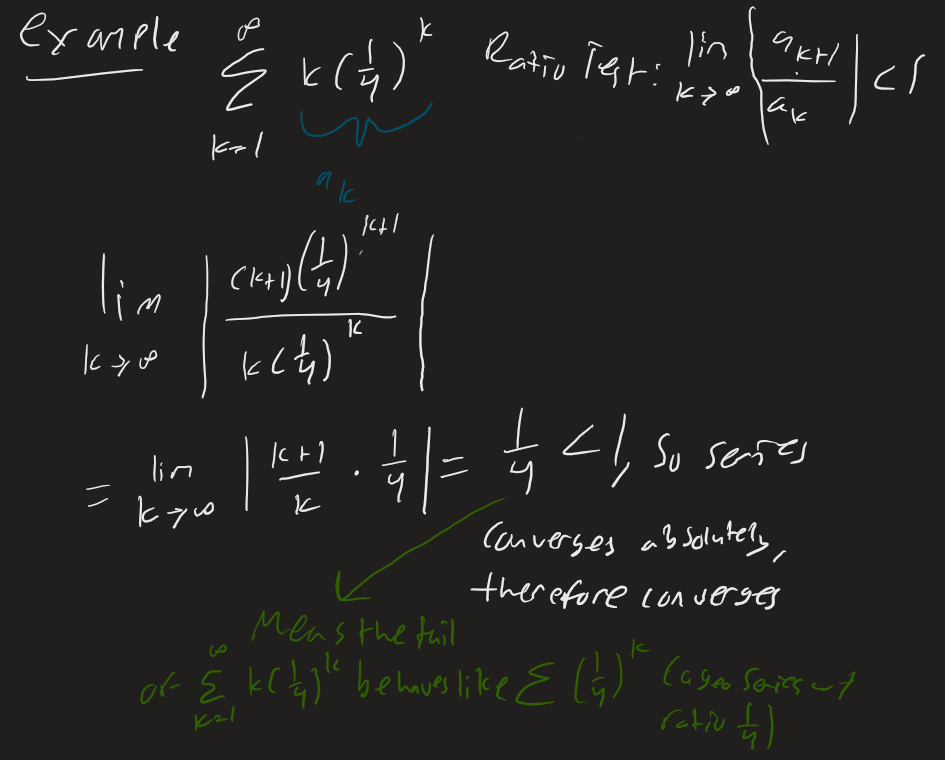
The ratio test is generally bad with things that look like p-series, in those cases its better to use the p-series test or a comparison test