#DataStructure#Computer-Science#CS251
Red-Black trees are a type of Binary Search Tree where something is balanced. They are not balanced in the same type of way, however it preserves logarithmic height
 We impose additional constraints to solve a problem, creating a red-black tree.
We impose additional constraints to solve a problem, creating a red-black tree.
Properties
- Every node is either red or black (highlight and bold since I can’t do red/black in here)
- The root is black always
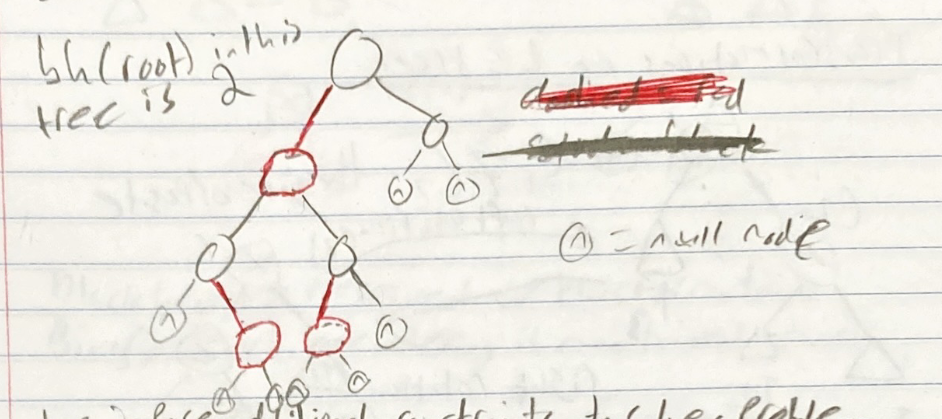
- Every null node is black. Look at the n’s in the tree above
- If a node is red, both the children are black
- There’s never two consecutive red nodes
- All paths from the root to null nodes have the same number of black nodes
- This is what creates a type of balancing
- The number of black nodes is called the black height
bh(node x)= # of black nodes on any simple path down to a leaf, NOT includingx- Black height is not necessarily the same as the height
- In our example above, the height of the tree is 2, but the black height of the root is 2
- From this property, we can claim that
- If h is logarithmic, so is insert, search, remove etc.
Transformations

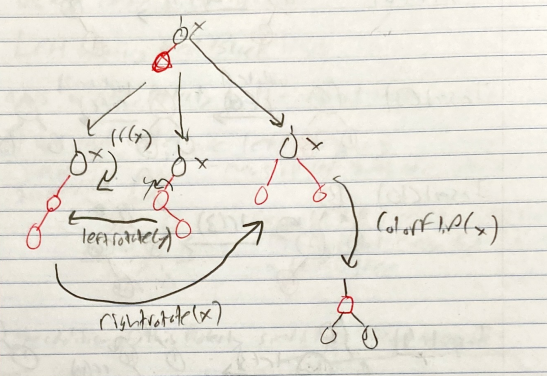
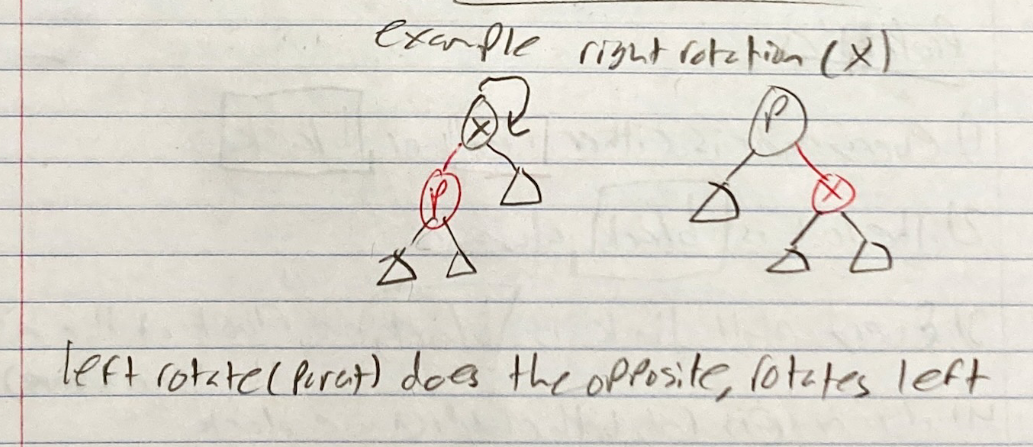
- Left and right rotation
- The colors of the nodes Z and X have to be different
- The only node that swaps parents is T2
- We visually rotate the node right or left
- These two functions are inverses, so doing them one after another on the same node results in where you started. Like adding and subtracting 2

- Color flip
- Color flip will swap the color of x and swap the color of x’s children
- You have to make sure that black height and all the other properties are properly maintained
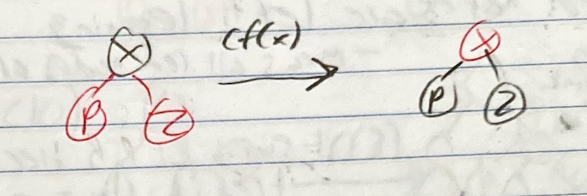
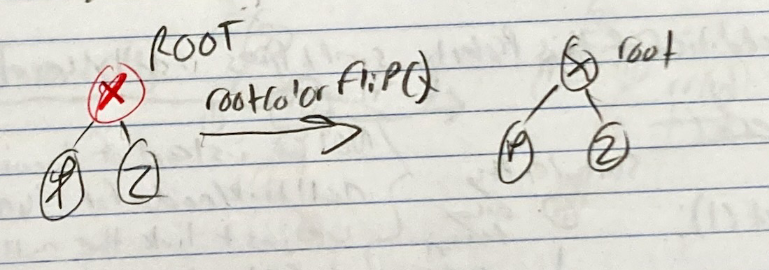
- Root color flip
- Just swap the color of the root
- Same thing as color flip (and left/right rotations) always make sure you maintain the properties of a red-black tree
Black height and binary search tree ordering is preserved with all of these transformations.
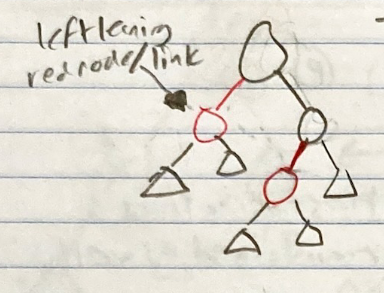
Left Leaning Red Black Trees
Because Red Black trees are normally VERY annoying to work with, we focus on left leaning red black trees. This adds a new property to the previous 5.
6. All red nodes are left leaning
- Means all red nodes are left children
- Every LLRB tree is a valid RB tree, but NOT every RB tree is a valid LLRB tree
-  The addition of this property simplifies insertion and deletion
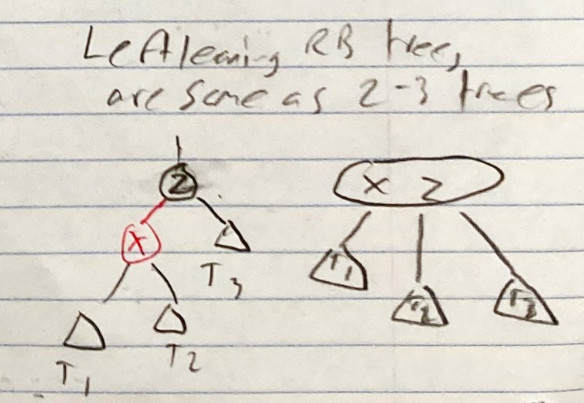
Left leaning red black trees can be converted to 2-3 Trees and vice versa.
The addition of this property simplifies insertion and deletion
Left leaning red black trees can be converted to 2-3 Trees and vice versa.
Insertion
- Insert in Binary Search Tree order, left child < node < right child
- Make sure to fix trees into Left Leaning Red Black Trees
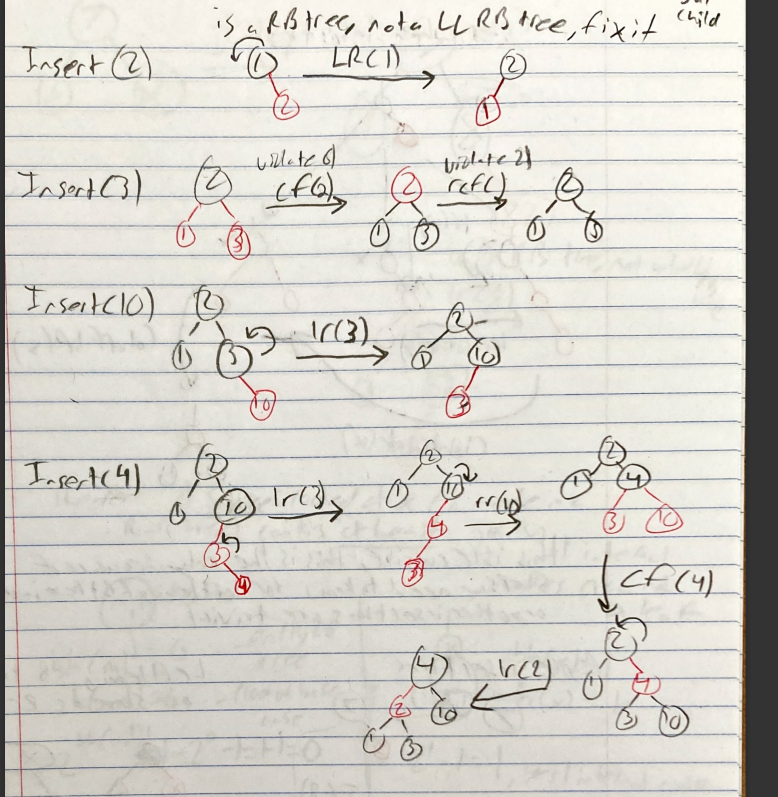
- These are all the cases when inserting
- This is recursive, this is the only sequence of steps you have to know for left leaning red black tree insertions. Any other insertions are trivial
- Theorem: A subtree rooted at x (a node in a Red Black Tree) contains at least internal nodes (aka not leaves)
Deletion
- ONLY EVER DELETE RED LEAVES!
- If it’s not a red leaf, use transformations to make it a red leaf and then cut it
- Another deletion technique is Lazy Deletion
- Here we don’t remove items but instead label them as removed
- Don’t allow too many deleted nodes