Comparison Tests

#Calc-2#Math#Series

Direct Comparison Test §

Look at the series $\sum _{k=1}^{\infty }\frac{1}{k^3+5}$ . The series passes the divergence test, the limit = 0. So it MIGHT converge. BUT the integral is very hard, so the integral test is not a good choice.

Notice however, that $\frac{1}{k^3+5}$ “looks like” $\frac{1}{k^3}$

Furthermore, notice that $\frac{1}{k^3+5}<\frac{1}{k^3}$ for all $k\ge 1$

$\sum _{k=1}^{\infty }\frac{1}{k^3}=1+\frac{1}{8}+\frac{1}{27}+\frac{1}{64}+...$ §

$\sum _{k=1}^{\infty }\frac{1}{k^3+5}=\frac{1}{5}+\frac{1}{13}+\frac{1}{32}+\frac{1}{69}+...$ §

So, $\sum _{k=1}^{\infty }\frac{1}{k^3+5}<\sum _{k=1}^{\infty }\frac{1}{k^3}$ The series $\sum _{k=1}^{\infty }\frac{1}{k^3}$ converges, as it is a p-series with $p>1$, so it converges Therefore, the series $\sum _{k=1}^{\infty }\frac{1}{k^3+5}$ is less than some finite #, so it must converge

Example §

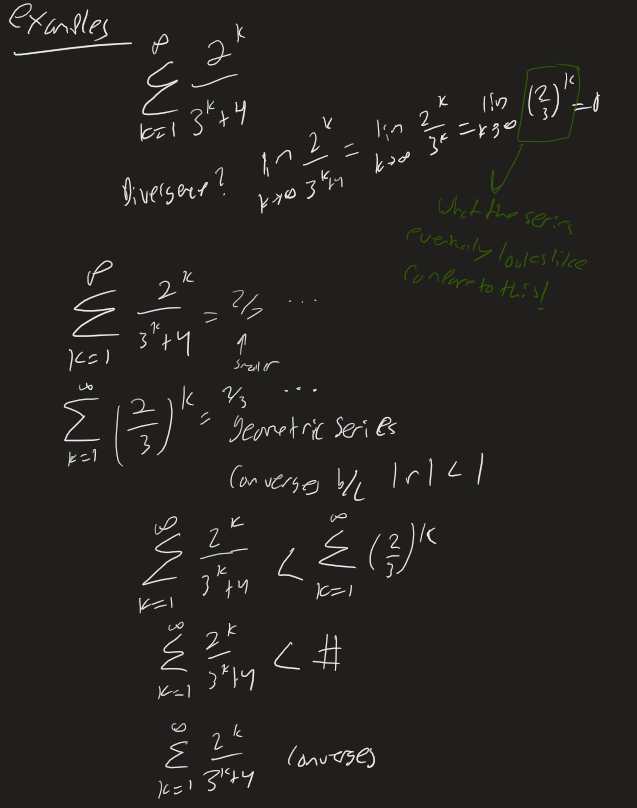
Limit Comparison Test §

There is another version of the comparison test.

If $\sum a_k$ is unknown and $\sum b_k$ is a known series, then you can compare the ratio of the limits of the two general terms

If ${\lim }_{k\to \infty }\frac{a_k}{b_k}=c$ (a finite number)

Then both series either converge or both series diverge.

Why? Because ${\lim }_{k\to \infty }\frac{a_k}{b_k}=c$ implies that the traits of each series are similar.