List and Queue Manipulation

From Operating System Design The Xinu Approach - By Douglas Comer §

Douglas Comer - Operating System Design The Xinu Approach (2015 Chapman and Hall)

• Linked List processing is fundamental in operating systems
• Linked structures enable a system to manage sets of objects efficiently
• This chapter will provide functions that make up a linked list manipulation system

A Unified Structure for Linked Lists of Processes §

• A process manager handles objects called processes
• At any time, a process only appears on one list
  • A process manager often moves processes from one list to another
  • Process managers don’t store all details of a process, only the process ID
• Process ID - a small non-negative integer used to reference the process
  • Process and Process ID are used interchangeably throughout this chapter (and as such this notes page)
• Linked lists in XINU were originally used in many places, however it quickly became clear the need to centralize it and have a single set of functions to handle everything
• To accommodate all cases, the following properties were selected and apply to all the linked lists
  • All lists are doubly linked, each node points to its predecessor and successor (parent and child, before and after, previous and next)
  • Each node stores a key as well as a process ID, even though the key is ignored in a First In First Out (FIFO) list
  • Each list has a head and a tail node; the head and tail nodes have the exact same memory layout as the other nodes
  • Non-FIFO lists are ordered in descending order; the key in the head node is greater than the maximum valid key, and the key in the tail node is less than the minimum valid key.
    • Presumably this is to keep the head and tail always the same, since a node will never be inserted with keys less than or greater than their values
• 
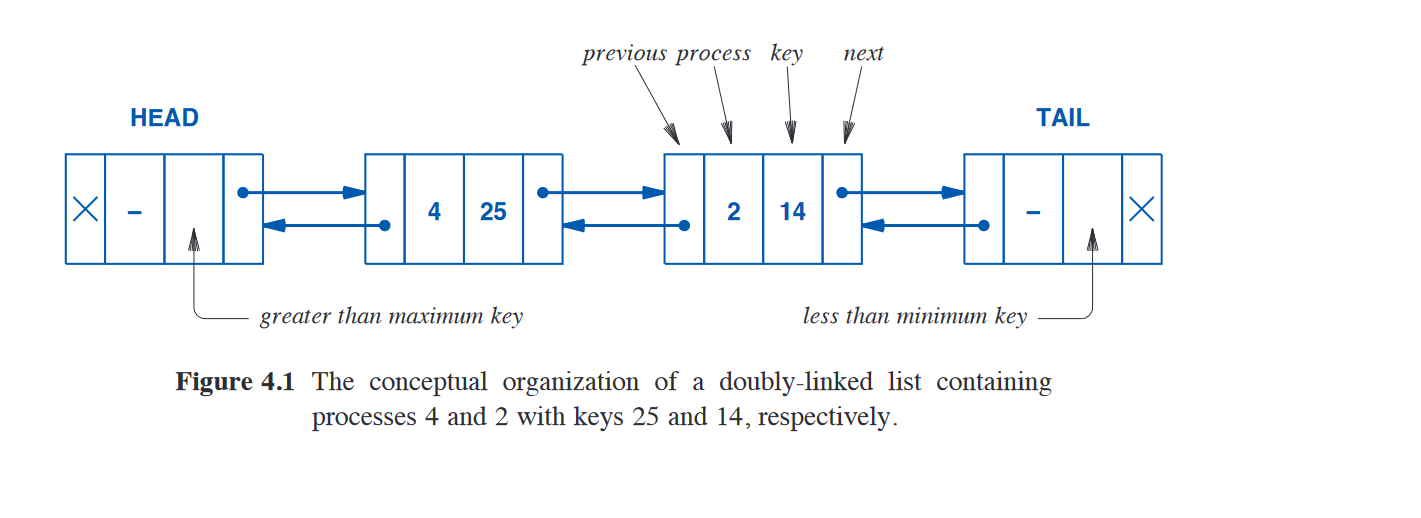
  • An example of a linked list data structure
  • Note: the next and previous for the tail and head respectively are set to null, the list does not loop back around
  • As such, an empty linked list would look like the following
  • 

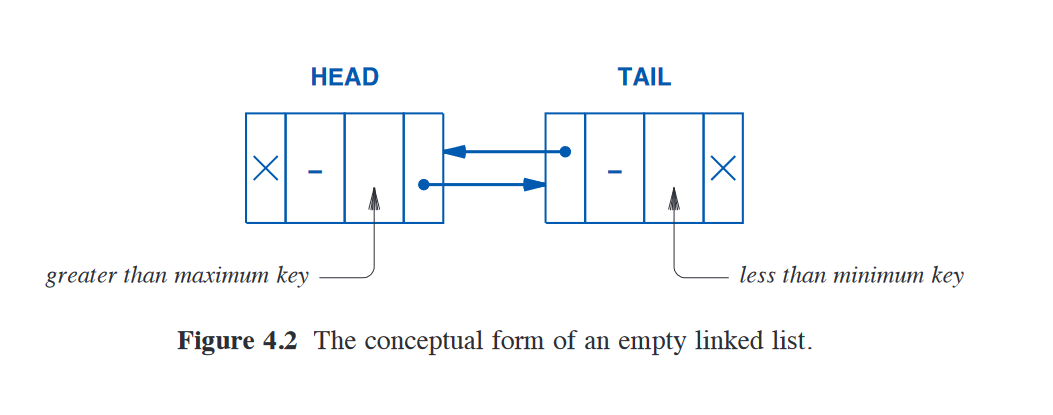
A Compact List Data Structure (Optimizing Memory) §

• One of the main things we want to do with embedded systems is reduce memory use
• In XINU, for the linked list implementation, this is done in two ways
  • Relative pointers
  • Implicit data structure

Note

It is important to know, that most operating systems place a fixed upper bound on the number of processes in the system. In XINU, the constant NPROC specifies this number of processes. As such, the process id’s can range anywhere from $0$, through $NPROC-1$ Most of the time in embedded systems NPROC is a small number, less than 100. This small limit is what enables the optimizations to work well

Relative Pointers §

• On a 32 bit architecture, pointers would each occupy four bytes
  • This means that each node of the linked list would have to take up a minimum of 8 bytes, without storing any additional data other than a next and previous pointer
• Instead of using pointers and storing nodes in various locations in memory, we can make use of an array and store the nodes in a contiguous memory location
• This lets us use indices of the array as references instead, we can essentially use the array index instead of a pointer
• We only want to do this if the system contains fewer than 100 nodes however, I assume if you go larger than 100 nodes the memory saved is no longer worth it

Implicit Data Structure §

• The second optimization lets us omit the process id field from all nodes, saving more space per node. This is possible because we know for a fact that a process can only appear on one list at a time

• To omit the process id, we use the array implementation described in the relative pointers and implicitly decide that the $i^{th}$ element of the array represents the process with process id $i$

  • For example, to put process id 3 on a particular linked list, we would insert node 3 into the list. That is, we would populate index 3 of the array and update the next/previous “pointers” (also using array indices as described previously) of everything
  • Thus, the relative address of a node is the same as the ID of the process being stored. The node at a relative address within the array of 53 is representing the process with the id 53

• 

  • The picture above shows the first picture (4.1) converted into an array format

Matthew's Interpretation

It almost makes sense to think of the next and previous references within our linked list more as the next process and previous process, since they end up referring to the next process id and previous process id rather than a pointer to a node. Accessing the array at that index will give you the key of that process along with it’s next and previous process id. The head and tail are stored past NPROC-1 so that they are known to not be process id’s and instead markers for the list itself

• XINU uses the term queue table to refer to the array storing the linked list

Implementation of the Queue Data Structure §

• The queuetab array contains NQENT entries
• As shown in figure 4.3, there is an implicit boundary between element $NPROC-1$ and element $NPROC$. Each element below the boundary corresponds to a process ID, and the elements above it (queuetab[NPROC] through queuetab[NQENT]) correspond to the heads or tails of lists
• This file is the file queue.h, since it ends in .h the file will be included in other programs. It contains global data structures, symbolic constants, and other inline functions (macros) that operate on data structures
• queuetab is first defined as an external (global) variable, so every process will be able to access the array
• The EMPTY, MAXKEY, and MINKEY values are all defined here
• NQENT defines the total number of entries in the queuetab array, and is conditionally defined
  • This lets the user define it somewhere else and change the queuetab array size without modifying this file
  • NQENT is assigned a value $NPROC+4+NSEM+NSEM$ which allocates enough entries in queuetab for NPROC processes plus head and tail pointers for NSEM semaphore lists, a ready list, and a sleep list
• The contents of entries in the array are defined by the qentry structure
  • qnext gives the relative address of the next node on a list, and qprev respectively does the previous
  • qkeycontains an integer key for the node
  • When a field, such as forward or backward pointer, does not contain a valid index value, the field is assigned the value EMPTY defined earlier
• The macros
  • queuehead - queuehead is passed in as q and as such, it can just be the value returned. I believe this is used to make other things more readable
  • queuetail - this initially confused me, but look at the implementation in Figure 4.3. The tail of the list is the node directly following the head of the list in our array. As such, adding 1 to the passed in queue head will result in the tail being returned.
  • firstid, lastid, firstkey, and lastkey are all fairly obvious implementaitons. The important thing to realize is that due to the implementation of the list, none of these values will ever fail or cause errors. The qkey and qnext/qprev values will always be defined, even in the case of the list being empty, since the head and tail also have them defined.
  • isempty and nonempty are a little trickier. Remember that the head and tail of the list are stored past NPROC in terms of their index. firstid of q refers to the next value from the head of the list. So if we’re checking if the list is empty, we want to know if the next node after the head is the tail. If its id (index) is greater than or equal to NPROC then that is the case. nonempty does the same thing but flipped, if the next node after the head has a process id/index less than NPROC then it must be the case that the list is not empty.
  • isbadqid(x) - This just checks if the given qid (index within the array) is less than 0 or greater than the arrays length (NQENT - 1)

Getting a Process from the list §

Extracting an item from the head of a FIFO Queue results in removing the item that has been in the queue the longest. For a priority queue, extracting from the head produces an item with the highest priority. Similarly, extracting from the tail would get the thing with the lowest priority. As such, we have three basic functions to handle extraction

• getfirst - get the process at the head of the list
  • takes a queue id as an argument, verifies that it represents a non empty list, finds the thing at the head of that list, and calls get item to get that thing
• getlast - get the process at the tail of the list
  • does the same thing as getfirst but gets the tail instead of the head
• getitem - get the process at an arbitrary point in the list
  • takes a process id as an argument and extracts the process from the list in which it is linked
  • this takes it out of the list hence why we set the previous values next to the items next and the next values previous to our previous
  • we then return the process id that is being extracted from the list The code for these functions is found in getitem.c shown above

FIFO Queue Manipulation §

Many of the lists in the process manager are First in first out queues. New items are inserted at the tail of the list, and items are always removed from the head of the list. Functions enqueue and dequeue allow us to implement these operations.

• dequeue takes a single argument that gives the id of the list to use and pulls out the value just after the head of the list
• enqueue takes two arguments, the id of the process to be inserted and the id of a list on which to insert it
  • it calls isbadpid to ensure that the pid passed in is valid. isbadpid will both check that the id is in the correct range (isbadqid) and that a process with that id exists The above is the file queue.c containing the logic for enqueue and dequeue. The file includes xinu.h which includes the complete set of XINU include files.

/** xinu.h -- include all system header files **/
#include <kernel.h>
#include <conf.h>
#include <process.h>
#include <queue.h>
#include <resched.h>
#include <mark.h>
#include <semaphore.h>
#include <memory.h>
#include <bufpool.h>
#include <clock.h>
#include <ports.h>
#include <uart.h>
#include <tty.h>
#include <device.h>
#include <interrupt.h>
#include <file.h>
#include <filesys.h>
#include <disk.h>
#include <lfilesys.h>
#include <ether.h>
#include <net.h>
#include <ipp.h>
#include <arp.h>
#include <uddp.h>
#include <dhcpp.h>
#include <icmp.h>
#include <tcp.h>
#include <name.h>
#include <shell.h>
#include <date.h>
#include <proctypes.h>
#include <delay.h>
#include <pci.h>
#include <quark_eth.h>
#include <quark_pdata.h>
#include <quark_irq.h>
#include <multiboot.h>
#include <stdio.h>

Manipulation of Priority Queues §

• A process manager often needs to select a process that has the highest priority
• As such, the linked list needs to be able to maintain priority of each process
  • In our example, the key is what is used to assign the priority
• A data structure that does this, maintains some kind of priority of its entries, is known as a Priority Queue
• Deletion from an ordered list is obviously trivial, you just remove the highest priority node from the list, which will always be at the front of the list
• Insertion is a bit different, since we want to insert things into the list based on their priority. We wouldn’t want to just always insert blindly to the back of the list
• insert takes in the id of a process to be inserted, the id of a queue to insert it on, and an integer priority for the process
  • insert uses the qkey field in queuetab to store the process’s priority. To find the correct location, it searches for an existing element with a key less than the key being inserted. During the search, curr moves along the list. The loop eventually will end because the tail element will always contain a value less than the smallest valid key. Once the correct location is found, the pointers are updated to link the new node onto the list

List Initialization §

• Everything described above assumes that the queue exists, even though it may be empty

Design Process

Initialization should be the final step in the design process of a data structure like this. First, design the data structures needed when the system is running, and then figure out how to initialize those data structures. This helps you separate the “steady state” of the system from the “transient state” and lets the designer focus on the most important aspect of the design, how it works, rather than sacrificing good design for easy intialization

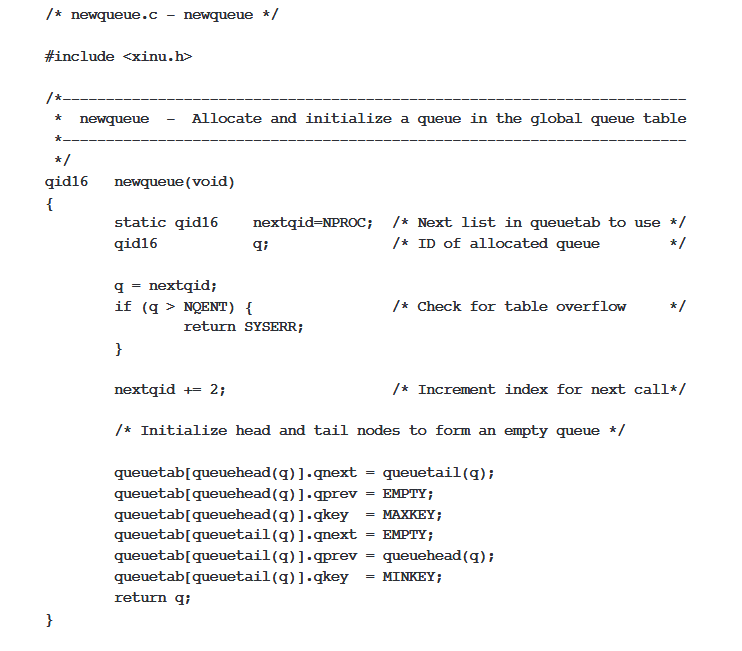
Initialization of entries in the queuetab structure are done on demand. A running process calls newqueue to create a new list. The system maintains a global pointer to the next unallocated element of queuetab which makes it easy to allocate the list. The head and tail of a list within the queue table could be allocated from any of the unused entries, however we optimize storage by requiring them to be successive locations within the array and identifying lists by the index of their head.
In the code, newqueue allocates two adjacent positions in queuetab for the head and tail nodes, and initalizaes the list to be empty via pointing them to each other. It assigns the value EMPTY to unused pointers. It also sets the key fields in the head and tail to the maximum and minimum integer values, respectively, with the assumption that neither will ever be used as a key. We only need one allocation function since our same list data structure can be used as either a FIFO queue or a priority queue, based on the functions you call on it for inserting/removing things. Once it finishes, newqueue returns the index of the list head to its caller. The caller only needs to store the location of the head, since the tail is computed by just adding one to the location of the head. Remember that all our locations are done via references within the array rather than actual pointers.

Summary (Taken straight from the book) §

The chapter describes a set of linked-list functions used to store processes. In our example system, linked lists of processes are kept in a single, uniform data structure, the queuetab array. Functions that manipulate lists of processes can produce FIFO queues or priority queues. All lists have the same form: they are doubly linked, each has both a head and tail, and each node has an integer key field. Keys are used when the list is a priority queue; keys are ignored if the list is a FIFO queue. The implementation uses a single array for all list elements — an entry in the array either corresponds to a process or to a list head or tail. To reduce the size required, the Xinu implementation uses relative pointers and an implicit data structure. In addition, the head and tail of a list are allocated equentially, allowing a single relative pointer to identify both the head and tail.