#Calc-2#Math#Vectors Scalars: (numbers) 5, -13, etc
- have magnitude only
- no sense of directions Compare to vectors, for example, I am traveling at 65 mph north
- There’s a sense of magnitude - 65 mph
- and a sense of direction - north
Mathematically, vectors are represented by arrows
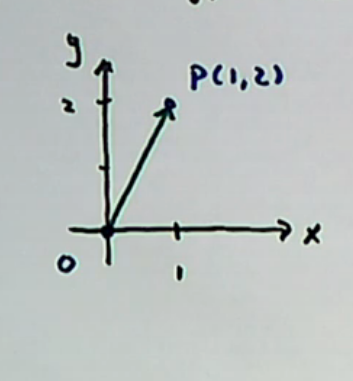 written as vector , put the point you start at, then the point you end at, and put an arrow on top
vector
^ this is how far to move right, the other number is how far to move up
i indicates a vector in the x direction, j a vector in the y direction, and k (not here yet) in the z direction
written as vector , put the point you start at, then the point you end at, and put an arrow on top
vector
^ this is how far to move right, the other number is how far to move up
i indicates a vector in the x direction, j a vector in the y direction, and k (not here yet) in the z direction
in general, <destination x - starting x, destination y - starting y>
What about vector
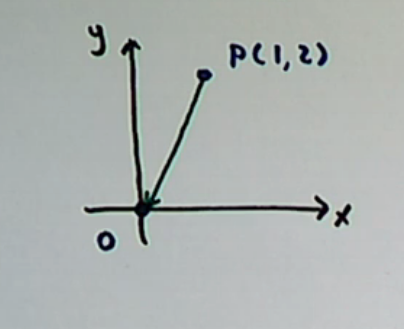
Note: In general, multiplying a vector by -1 reverses its direction while keeping the magnitude the same
Multiplying by scalars
very simple to do
This changes the magnitude (length of the vector) by a factor equal to the scalar
reverses OP’s direction and lengthens it by a factor of 3
Finding Magnitude
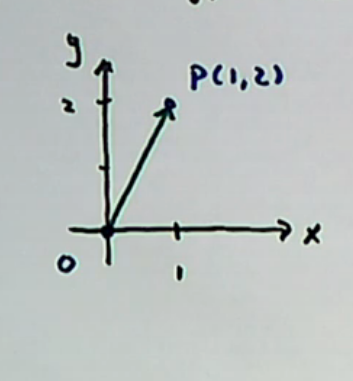
To find the magnitude (length) of vector OP, written as
There’s a right angle triangle in there! We know the base and the height, so the magnitude is
Generalized, if , then the magnitude is
Moving Vectors
Copies of the same vector at different locations are equal
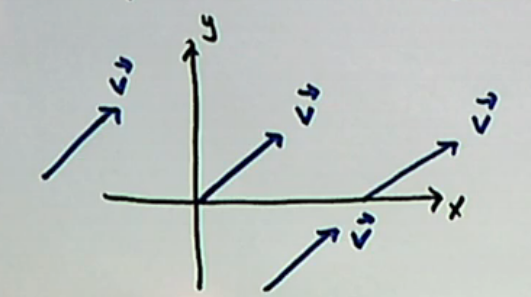 Each of these is called a position vector
(gives the relative difference between start and end)
Each of these is called a position vector
(gives the relative difference between start and end)
Even if a vector is moved, they are the same as long as they have the same magnitude and direction
Two Vectors are equal if they have the same magnitude and the same direction
Vector Operations
Adding and Subtracting vectors
Algebraically, very easy
Graphically, things get more interesting
When adding, keep first vector the same and move the second vectors tail to the head of the first. Create a new vector from the tail of the first vector to the head of the second to get the final vector result.
 This is called the Triangle Rule
This is called the Triangle Rule
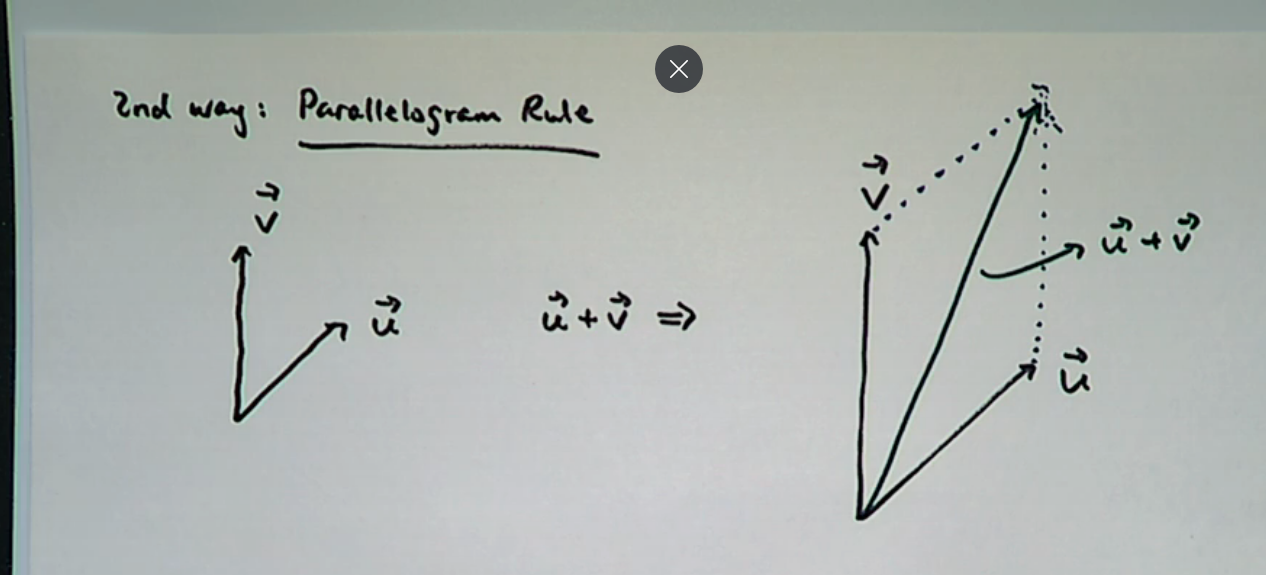
Another way called the Parallelogram Rule
It basically does the same thing, just looks a bit different.
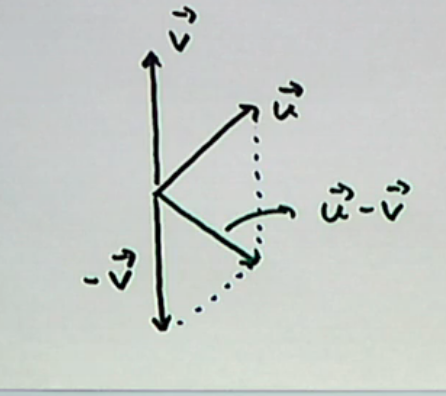
Subtraction graphically looks like doing
Multiplying, just look at scalars above its that
Dot Product and Cross Product
Unit Vectors
These are vectors with a magnitude of 1
The general unit vectors are (the parentheses are only for 3D vectors, as is the )
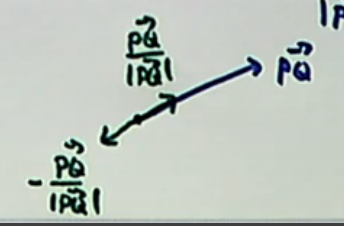
A unit vector parallel to is
Another one is