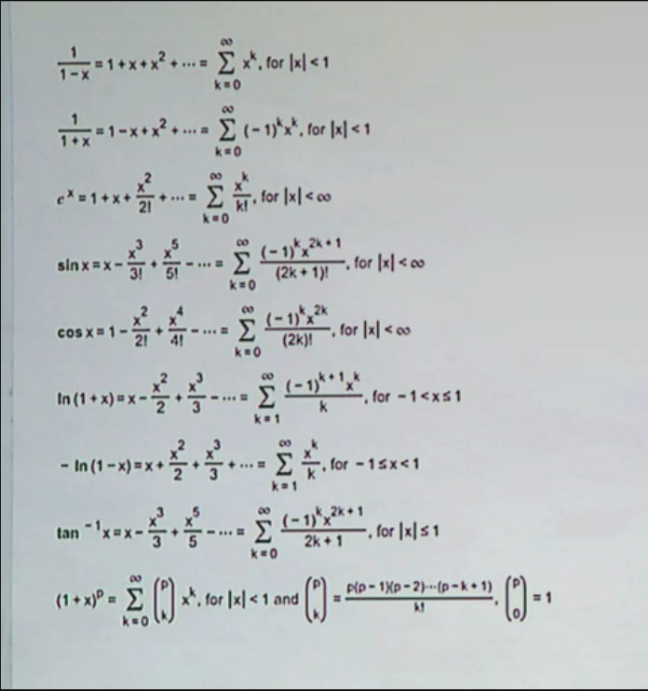Taylor Series

#Calc-2#Math#Series A Taylor Series is a type of Power Series

What are the $C_k$’s of the Taylor Series?

The idea with a Taylor series is that it should behave similarly to it’s corresponding f(x) => The way we do this is we match all the derivatives at x = a

The coefficients of the Taylor Series look like $C_k=\frac{f^k(a)}{k!}$

Taylor Series of f(x) at x=a $\sum _{k=0}^{\infty }\frac{f^{(k)}(a)}{k!}(x-a{)}^k=f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{\prime \prime \prime }(a)}{3!}(x-a{)}^3+...$ We have seen part of this before, if you chop the series off after the first derivative you get $f(x)=f(a)+f^{\prime }(a)(x-a)$ This is the Linear Approximation of f(x) near f(a)

So think of the Taylor Series as an extension of linear approximation. We use more derivatives to better capture the shape and behavior of f(x)

Example Finding Taylor Series §

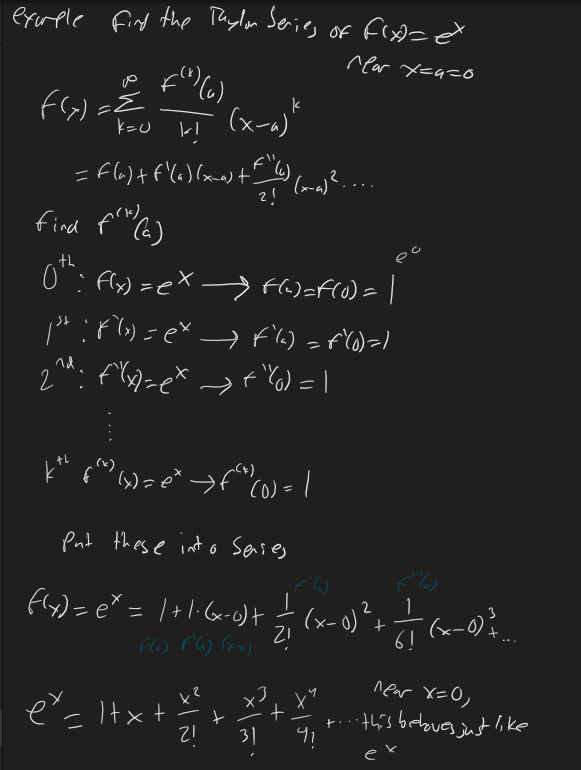
Taylor Polynomials §

If you cut off after the kth degree term, you get what’s known as the kth order Taylor Polynomial ($P_k$)

In the above example, the Taylor Polynomials are as follows, $P_0=1$ $P_1=1+x$ $P_2=1+x+\frac{x^2}{2}$ $P_3=1+x+\frac{x^2}{2}+\frac{x^3}{3}$ …

Taylor Remainder Theorem §

The Taylor Remainder is everything that we cut off from the series to make the Taylor Polynomial In general $f(x)=P_n(x)+R_n(x)$

For example, $P_2=f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2$ The remainder of it (the second Taylor Remainder) is $R_2=\frac{f^{\prime \prime \prime }(a)}{3!}(x-a{)}^3+\frac{f^{(4)}(a)}{4!}(x-a{)}^4+...$ The remainder is an infinite series which converges to something given by Taylors Remainder Theorem

Taylor Remainder Theorem says

$R_n$ converges to $R_n=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a{)}^{n+1}$ where $c$ is somewhere between $a$ and $x$

$c$ is usually very hard to find, so instead we usually just find the maximum value of the n+1’th derivative on the interval between x and a, calling that M. (Make sure to include the endpoints!)

We can use the remainder $R_n$ to estimate how much error is in the approximation of f(x)

$|f(x)-P_n(x)|=|R_n(x)|=|\frac{f^{(n+1)}(c)}{(n+1)!}(x-a{)}^{n+1}|$ so long as $a\le c\le x$

Examples can be found Day 28 of Calc 2  §

Maclaurin Series §

A Maclaurin Series is literally just a Taylor Series where $a=0$. That’s it.

We use Maclaurin Series to find other Power Series’ like how we used $\frac{1}{1-x}$ in these examples