Heap Sort

#Sorting#Computer-Science#CS251 If we put n items into a max Heap, inserting all the items will take $O(n\log n)$ time, since each insertion is $O(\log n)$ and we do n of them. We can make an array from the max’s of the heap made form the input array to sort it. GetMax is $O(\log n)$ so repeating it n times for each item is $O(n\log n)$

Heap Sort is an in place algorithm

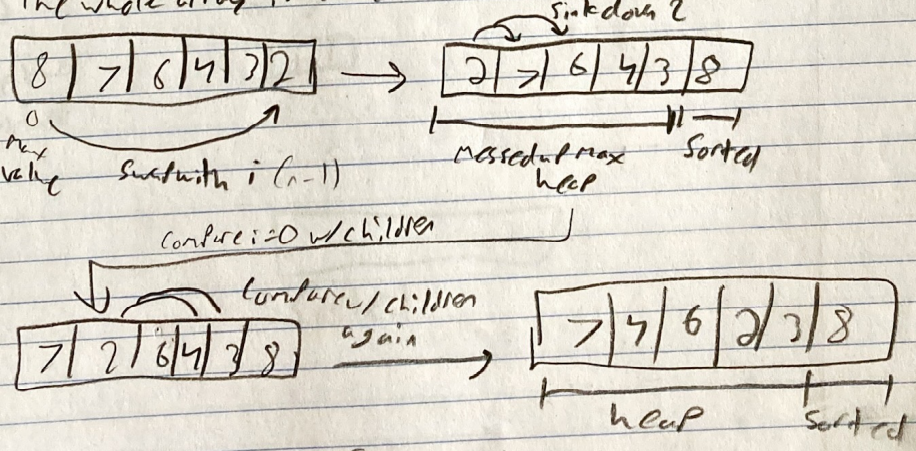
We turn the input array into a max heap, then get the max and put it at the end. Repeating this until the heap is empty results in a sorted array.

Pseudocode §

HeapSort(A: array of size n)
	buildHeap(A) // Turns A into a binary heap. Max heap for ascending order, Min heap for descending order
	for (i = n-1, i > 0, i -= 1)
		sortdown(A, i) // getMax and store it into index i
	endfor
end HeapSort

The array will be populated from right to left with the right part being sorted and left part as the remaining heap

buildHeap(A) §

Transforms array A into a binary heap

There are two approaches for making the heap

Top down approach §

We use

• left(i) = 2i +1
• right(i) = 2i+2
• parent(i) = $\lfloor \frac{i-1}{2}\rfloor$ to compare values in the heap and move them if needed.

We loop through the entire array, sinking/rising elements as needed until the array is in heap order.

These swaps will take $O(\log n)$ time.

Bottom up approach §

We start with the childless nodes and build up $\frac{1}{2}$ the heap will always be childless

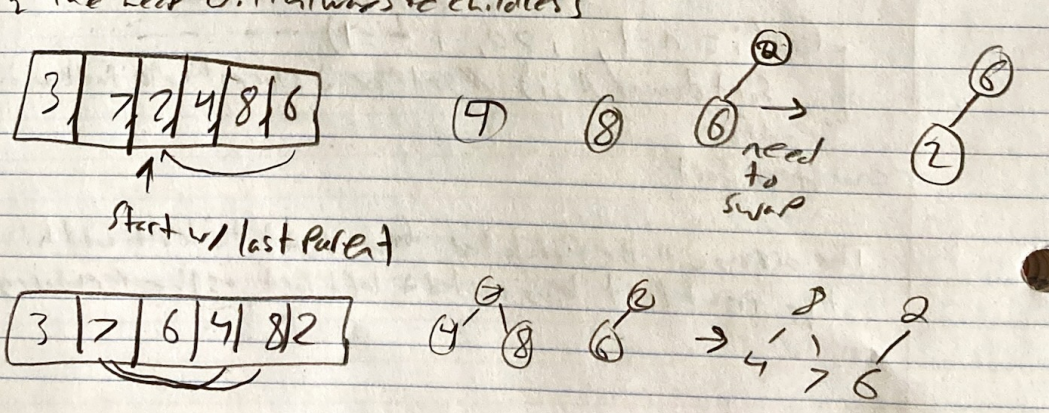
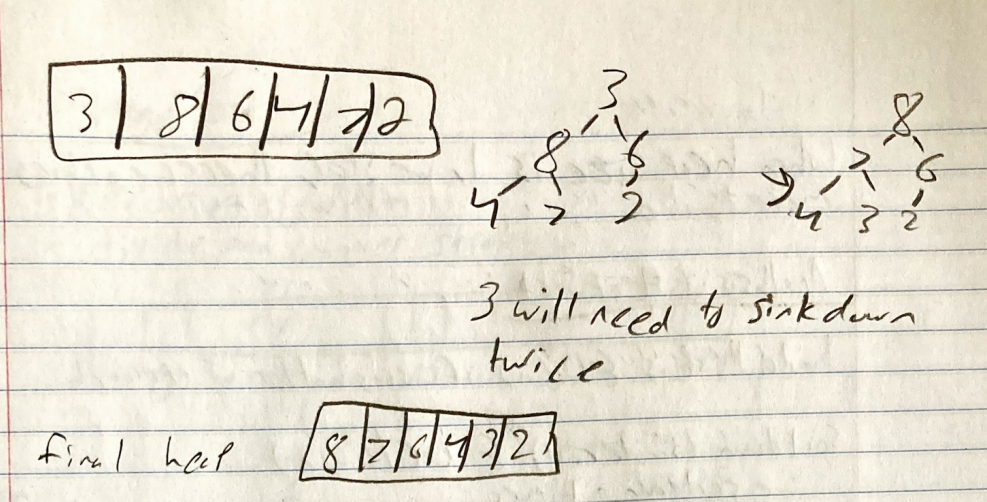
Basically we start at the bottom and sink down each parent if needed

This is overall faster than top down approach. It ends up being $O(n)$

SortDown(A, i) §

The whole array is a max heap at this point

This process repeats for every index resulting in a sorted array

When heap size is 1, we stop, there’s nothing more to do.

Analysis of Heap Sort §

buildHeap is $\in O(n)$ if using bottom up appraoch

sortDown (one call of it) $\in O(\log n)$ we sortdown n times -> $n\cdot \text{sortdown}\in O(n\log n)$ We also can’t do better than $n\log n$ so $\Theta (n\log n)$

In real life, heap sort isn’t great. The cache memory does not help, we jump back and forth between items often. OS’s don’t really like that. A better alternative is Merge Sort or Quick Sort