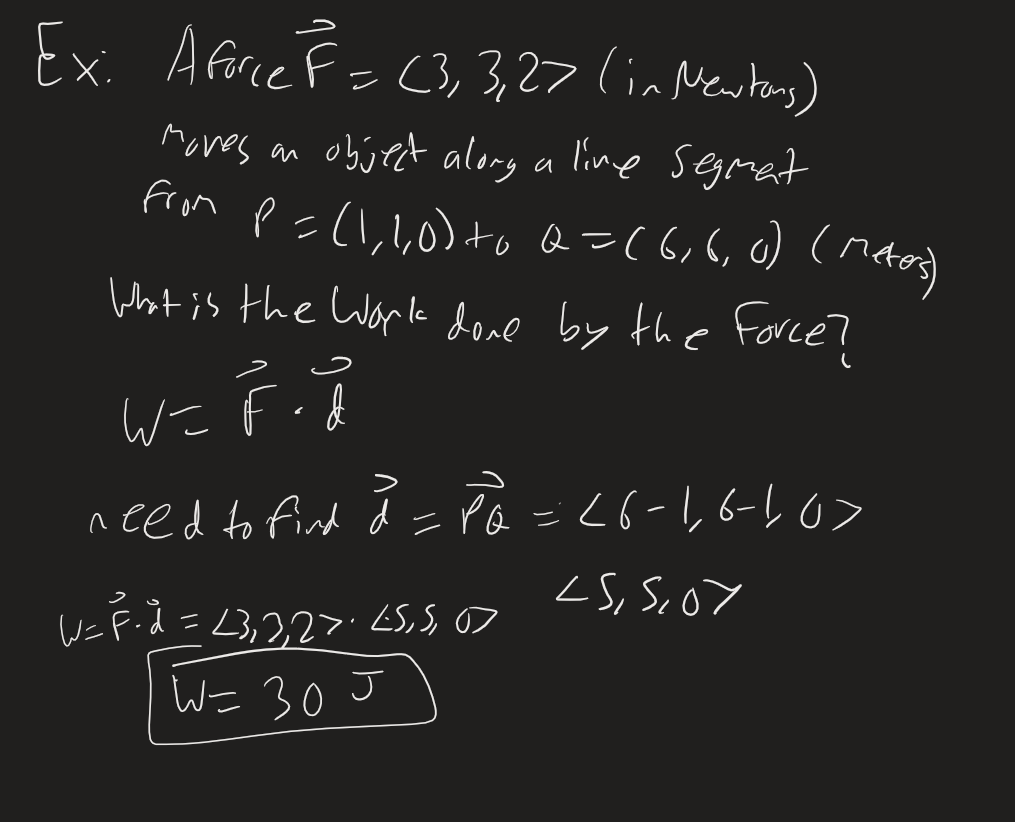Dot Product

#Calc-2#Math#Vectors Given 2 vectors, $\vec{u}=<u_1,u_2,u_3>$ and $\vec{v}=<v_1,v_2,v_3>$ the dot product is $\vec{u}\cdot \vec{v}=u_1{v}_1+u_2{v}_2+u_3{v}_3$

Dot Product is an operation on 2 vectors that results in a scalar, a single number.

Let $\vec{u}=<4,1,-2>,\vec{v}=<3,4,5>$ Then $\vec{u}\cdot \vec{v}=4\cdot 3+4\cdot 1+-2\cdot 5=12+4+-10=6$

Geometric Meaning §

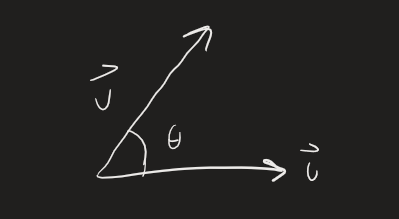
THEOREM: If $\vec{u}$ and $\vec{v}$ are nonzero vectors, then $\vec{u}\cdot \vec{v}=|\vec{u}||\vec{v}|cos\theta$ Where $0\le \theta \le \pi$

We can use this to calculate the angle $\theta$ between $\vec{u}$ and $\vec{v}$

${\cos }^{-1}\left(\frac{\vec{u}\cdot \vec{v}}{|\vec{u}||\vec{v}|}\right)=\theta$

Perpendicular Vectors §

• If the dot product of two vectors is 0, then those two vectors are perpendicular (not parallel)

Orthogonal Projection §

Two vectors are Orthogonal if and only if $\vec{u}\cdot \vec{v}=0$ Notation: $\vec{u}\perp \vec{v}$ Note: In 2D and 3D, two non zero orthogonal vectors are perpendicular to each other Orthogonal and Perpendicular are basically the same

The Orthogonal projection of $\vec{u}$ onto $\vec{v}$, denoted as $pro{j}_{\vec{v}}(\vec{u})$ where $\vec{v}\ne 0$ is $pro{j}_{\vec{v}}(\vec{u})=|\vec{u}|\cos \theta (\frac{\vec{v}}{|\vec{v}|})$ $|\vec{u}|\cos \theta$ represents the scalar length, and $\frac{\vec{v}}{|\vec{v}|}$ is the unit vector giving the direction

We can also use the formula $pro{j}_{\vec{v}}(\vec{u})=(\frac{\vec{u}\cdot \vec{v}}{\vec{v}\cdot \vec{v}})\vec{v}$ This formula is useful because we don’t need to calculate $\theta$. It works because if you convert the dot products to the previous definition, things cancel out leaving the original formula.

The scalar component of a vector $\vec{u}$ in the direction of $\vec{v}$ is $sca{l}_{\vec{v}}(\vec{u})=\frac{\vec{u}\cdot \vec{v}}{|\vec{v}|}$

Applications of Dot Product §

Dot Product can be used to find Work

Let a constant force $\vec{F}$ be applied to an object, producing a displacement $\vec{d}$. If the angle between $\vec{F}$ and $\vec{d}$ is $\theta$, then the Work done by the force is $W=\vec{F}\cdot \vec{d}$ The Force is in Newtons and the resulting scalar (Work) is in Joules