Non-Comparison Sorts

#Sorting#Computer-Science#CS251 Sorting without compares can be faster than $n\log n$, but it usually takes some assumptions

Counting Sort §

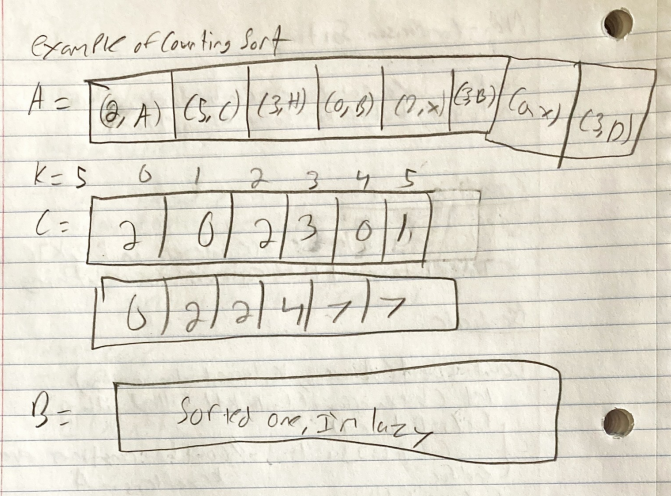
Counting sort assumes that the keys are integers within the range [0, k] The idea is to count the frequencies of everything

Pseudocode §

CountingSort(A: array, k: largest value in array)
	let C be an array of length k+1 filled with 0's
	for (i = 0 to n-1)
		C[A[i]]  += 1 // count how many times every key appears in A
	end for
	for (i = 1 to k)
		C[i] <- C[i] + C[i-1] // offset values in C to get the indices they'll go at
	endfor
	let B be an array of size n
	for (i = n-1 to 0)
		B[C[A[i]]-1] <- A[i] // figure out where the curent key is
		C[a[i]] -= 1 // put into a new array at position C-1, subtract 1 from C for next time
	endfor
	return B
end CoutingSort

Details §

This algorithm is not in place Counting Sort is $\in O(n+k)$ It only considers one dimension when sorting values and requires keys of integers [0, k]

Radix Sort §

A sort to sort multiple tuples worth of data

(4, 7, 9, 1) (4, 7, 9, 2) (5, 3, 2, 0) (5, 5, 5, 5) These tuples are sorted in lexicographic order

Lexicographic Order §

$(x_1,x_2,...,x_d)<(y_1,y_2,...y_d)$ is true if and only if $(x_i<y_i)\text{ OR }(x_1=y_1\text{ AND }(x_2,...,x_d)<(y_2,...,y_d))$

Pseudocode §

RadixSort(A: array of tuples with dimesnions d)
	for (i = d to 1)
		use a stable sort on A at dimension i
	endfor
end RadixSort

Example §