#Calc-2#Math#Vectors Cross Product is another operation that can be done on two vectors. The result of doing the cross product is another vector
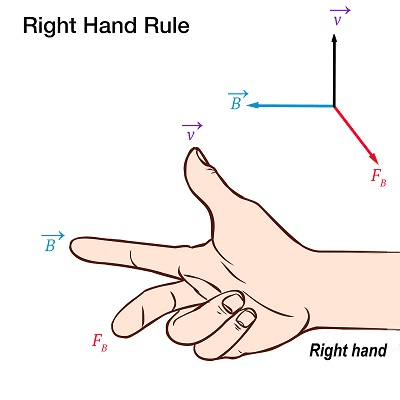
The magnitude of the cross product is given by The direction is given by the Right Hand Rule For , curl the first vector into the second using the fingers of your right hand. The direction of your thumb is the direction of ALWAYS USE THE RIGHT HAND FOR THIS
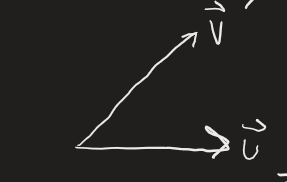 In this case, is coming out of the screen, since your thumb would be pointing straight up.
has your thumb pointing down, so points into the screen. Both cross products will have the same magnitude, but opposite directions
In this case, is coming out of the screen, since your thumb would be pointing straight up.
has your thumb pointing down, so points into the screen. Both cross products will have the same magnitude, but opposite directions
Order matters in cross products
Another note, and are perpendicular/orthogonal to both and
==The cross product of two parallel vectors is the 0 vector. ( or )==
The positions of the XYZ axes obey the right hand rule.

Finding the Cross Product
To find the cross product of two vectors, we use determinants.
Quick reminder on determinants:
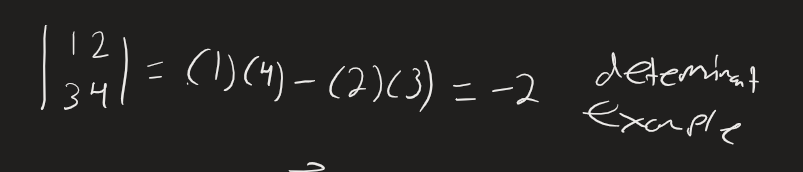
Here’s how we apply it using vectors to find the cross product.
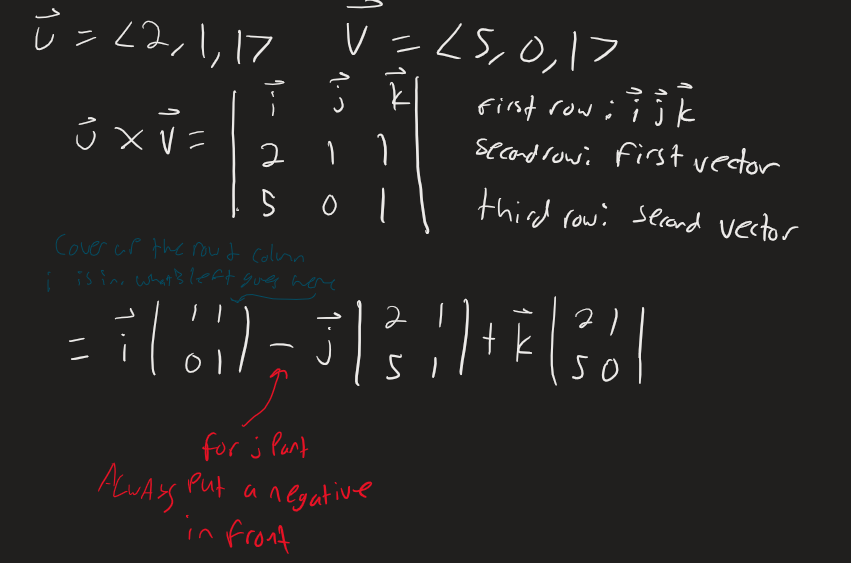
NOTE THAT FOR THE j PART WE ALWAYS PUT A NEGATIVE IN FRONT
After setting up the determinants like this, we then solve the determinants. So, using the above vectors is
, which can be found by flipping the signs of since its just the opposite direction
You can check if its perpendicular by taking the Dot Product of the Cross Product and one of its parts and so on
Applications of Cross Product
Area of Parallelogram
is the area of the parallelogram with adjacent sides and
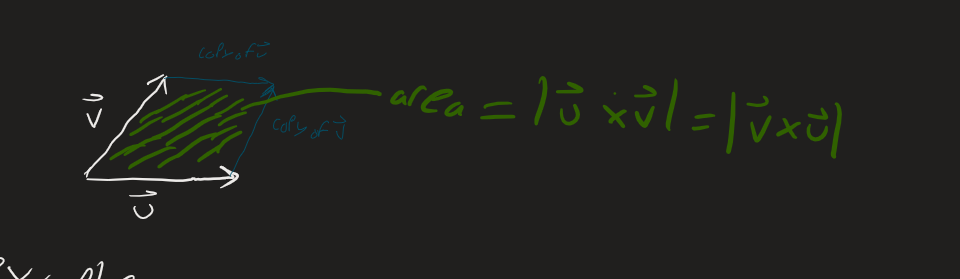
Collinear and coplanar vectors
If vectors and are on the same line (collinear) then because
If A,B,C, and D are all on the same plane (coplanar), then and are perpendicular to any vector on the plane, so and
Torque (or moment)
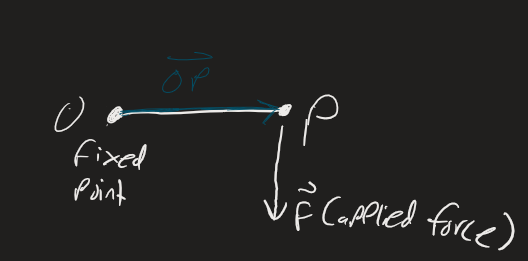
The Torque about the Point O is
Magnetic Force
A particle with charge is moving with velocity through a magnetic field The Force due to the magnetic field on the particle is found by