#DataStructure#Computer-Science#CS251
- Non-linear, top-down structures
- Trees are composed of a series of nodes that point to children (the node that points to children is called a parent)
- Trees can have 0 to many children
- Trees are part of the wider set of Graphs (They’re a type of graph)
Definitions
- Size: number of nodes in a tree
- Just count the number of nodes
- A tree is considered empty when there are 0 nodes in it
- Root: A node that has no parent nodes
- Usually the node at the top of the tree that all other nodes descend from
- Parent: Node that points to the current node
- Grandparent: Node that points to this nodes parent
- Sibling: Nodes other than the current node that the parent points to
- Children: Nodes that the current node points to
- Leaf: Node that has no children
- Height: Distance between lowest node and root node
- Height at the root is considered 0
- Depth: same as height
Binary Trees
- Special kind of tree where each node has either 0, 1, or 2 children
- We designate these children as left or right
- A full binary tree is a binary tree where every node has 2 children except for the leaves
- Properties of binary trees
- Given a binary tree of height h, the maximum number of leaves it can have is and the maximum number of nodes it can have is
Traversing Binary Trees
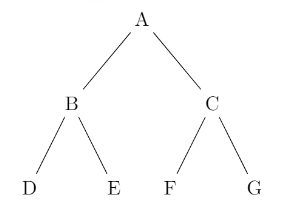
- (We will use the above tree as an example)
- Preorder - NLR
- Visit a node before its descendants (NLR)
- Example in above: A, B, D, E, C, F, G
- Inorder - LNR
- Visit a node before its right descendant but after its left descendant (LNR)
- Example in above: D, B, E, A, F, C, G
- Postorder - LRN
- Visit a node after its descendants (LRN)
- Example in above: D, E, B, F, C, G, A
- Levels
- Traverse the tree one level at a time from left to right
- Example in above: A, B, C, D, E, F, G
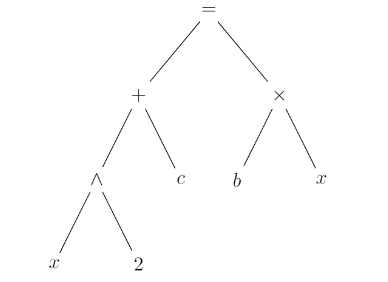
Expression Trees
We can build binary trees out of arithmetic expressions by creating splits at significant operators
- Converting into an expression tree would look like this