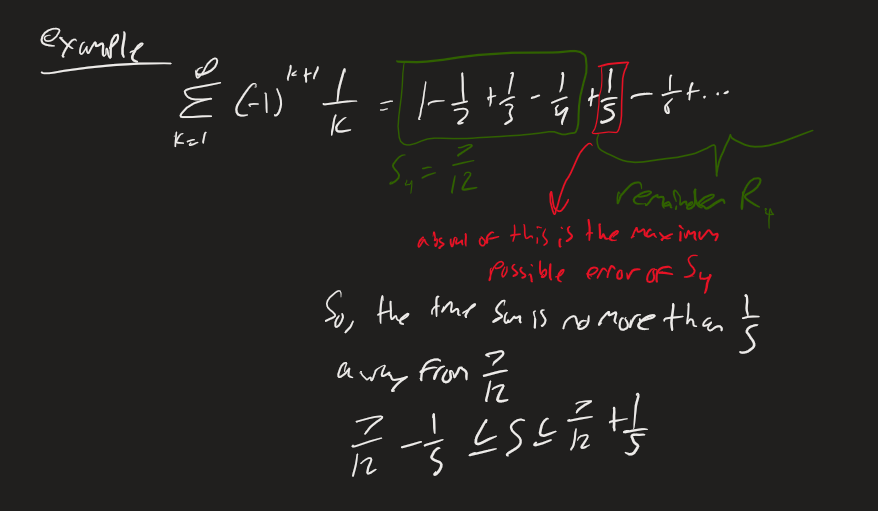Alternating Series

#Calc-2#Math#Series An Alternating Series is a type of series where each term has a different sign

$\sum _{k=1}^{\infty }(-1{)}^{k+1}\frac{1}{k}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-...$

The above series is known as the Alternating Harmonic Series (the one that doesn’t flip terms is the Harmonic Series)

The $(-1{)}^{k+1}$ changes the sign of each term

In General, alternating series usually look like

$\sum _{k=1}^{\infty }(-1{)}^{k+1}{a}_k$ or $\sum _{k=1}^{\infty }(-1{)}^k{a}_k$ where $a_k\ge 0$

An Alternating Series converges if the following conditions are met

1. The magnitude of each term is eventually non increasing $a_{k+1}\le a_k$ for $k\ge$ some number
2. ${\lim }_{k\to \infty }{a}_k=0$ (basically the divergence test)

These two things together are called the Alternating Series Test

Why? §

Look at $\sum _{k=1}^{\infty }(-1{)}^{k+1}\frac{1}{k}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-...$ It’s easy to see that the limit = 0 and that $\frac{1}{k}$ is non increasing for $k\ge 1$ so this series converges If you look at the series’ partial sums, you see that they get closer and closer to about 0.7

Example §

Estimating the sum of a convergent series §

We can estimate the sum of a convergent alternating series to be within any accuracy we want

Look at $\sum _{k=1}^{\infty }(-1{)}^{k+1}{a}_k$, assume it converges

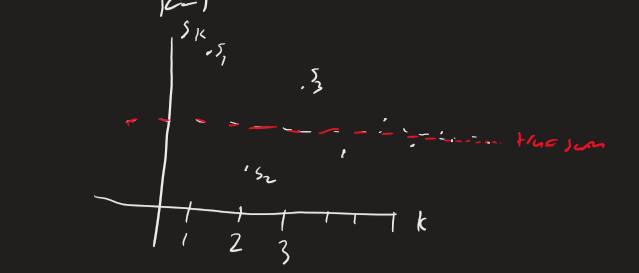
Note: the true sum is always between $S_{k+1}$ and $S_k$ $S_k\le S\le S_{k+1}$ where S is the true sum

If you subtract $S_k$ and take the absolute value, you end up with $0\le |S-S_k|\le |S_{k+1}-S_k|$ $S_{k+1}-S_k=a_k$ and $S-S_k$ is the remainder after the kth partial sum, $R_k$ this is how far the partial sum $S_k$ is from the true sum

So, $|S-S_k|\le a_{k+1}$ the error of the kth partial sum from the true sum is no bigger than the magnitude of the next term