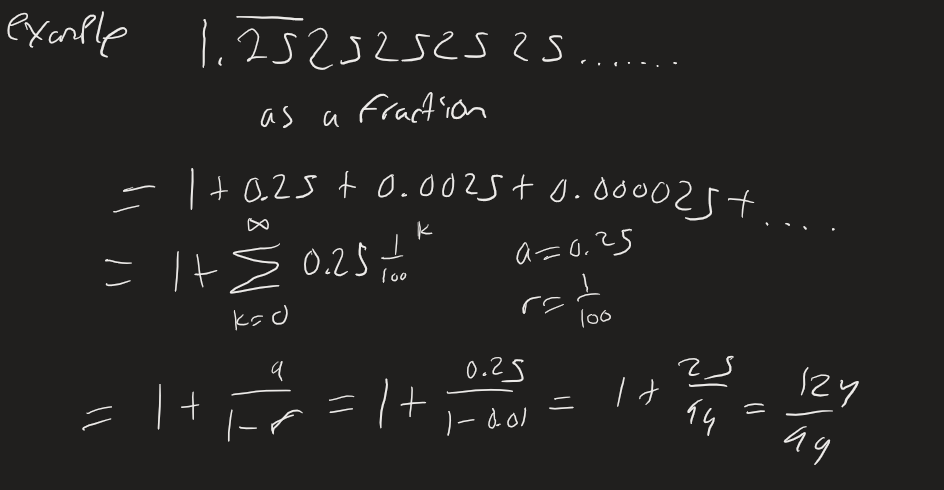Geometric Series

#Calc-2#Math#Series A Geometric Series is a type of Infinite Series In a Geometric Series, there is a consistent ratio between consecutive terms. For example $\frac{1}{4}+\frac{1}{12}+\frac{1}{36}+\frac{1}{108}...$ these can be written as $a+ar+a{r}^2+a{r}^3+...=\sum _{k=0}^{\infty }a{r}^k$ However, if k starts at 1, then it needs to be $\sum _{k=1}^{\infty }a{r}^{k-1}$

Partial Sum of Geometric Series §

To find the nth partial sum of a geometric series, you add up the terms from k=0 to k-1

$S_k=a+a+r+a+r^2+...+a{r}^{k-1}$

Manipulating this formula by multiplying it by r we get another formula,

$r\ast S_k=ar+a{r}^2+a{r}^3+...+a{r}^k$

Subtracting the second from the first results in this

$S_k-r{S}_k=a-a{r}^k$ $S_k(1-r)=a-a{r}^k$ $S_k=\frac{a-a{r}^k}{1-r}$

Another way of writing the formula:

$S_k=\frac{firstterm}{1-r}$ §

This formula gives the kth partial sum of a geometric series with common ratio r

Example

$\frac{1}{4}+\frac{1}{12}+\frac{1}{36}+...=\sum _{k=0}^{\infty }a{r}^k=\sum _{k=0}^{\infty }\frac{1}{4}{\frac{1}{3}}^k$ $a=\frac{1}{4}$, $r=\frac{1}{3}$

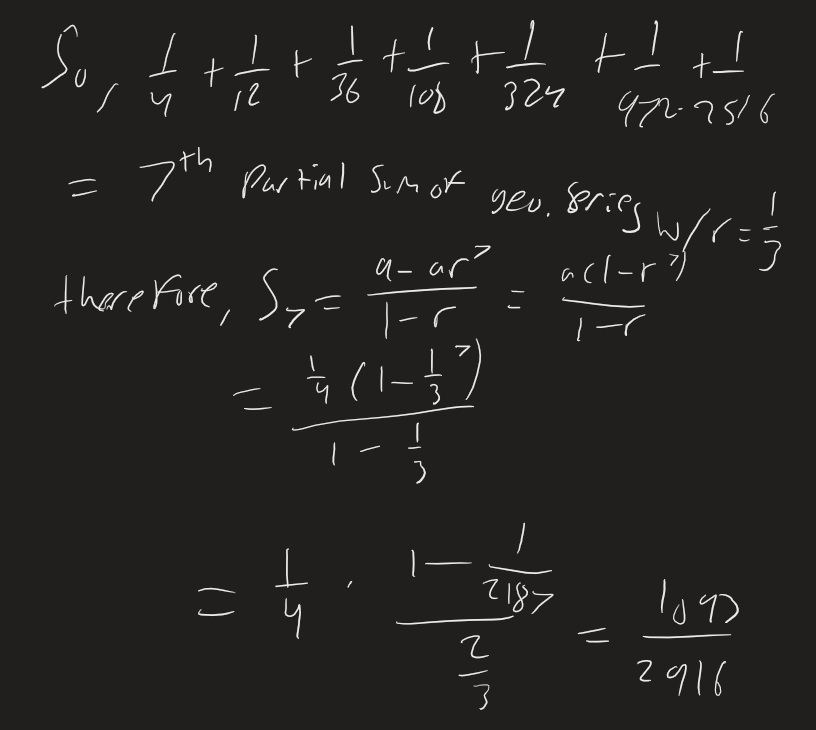
Convergence of Infinite Geometric Series §

What if we didn’t stop and continued adding? Would the series always converge? If so what would its sum be?

${\lim }_{k\to \infty }{S}_k={\lim }_{k\to \infty }\frac{a(1-r^k)}{1-r}$ for this limit to exist, the limit as k approaches infinity of $r^k$ has to be finite. If |r| < 1, the limit = 0. From this we get

An Infinite Geometric Series converges if the $|r|<1$ . A finite series will always converge.

Example

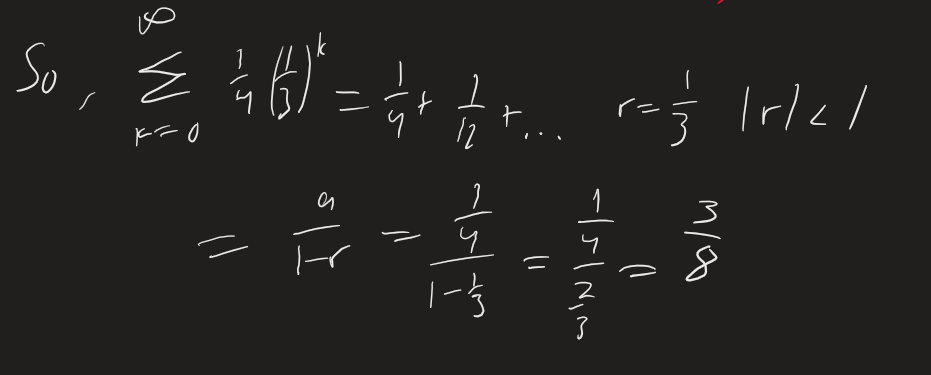
Using Geometric Series to rewrite decimals as fractions §