Sequences

#Calc-2#Math#Series Sequences Lecture Notes - Examples Here

A sequence is a list of of numbers in some particular order. For example $\{1,2,3,4,5,6,...\}$ or $\{2,4,6,8,10,12,...\}$

We can list the numbers in a sequence like above or by:

Explicit Formula §

A formula that can be used to generate each term in the sequence

$\{2,4,6,8,..\}=\{2n{\}}_{n=1}^{\infty }$ §

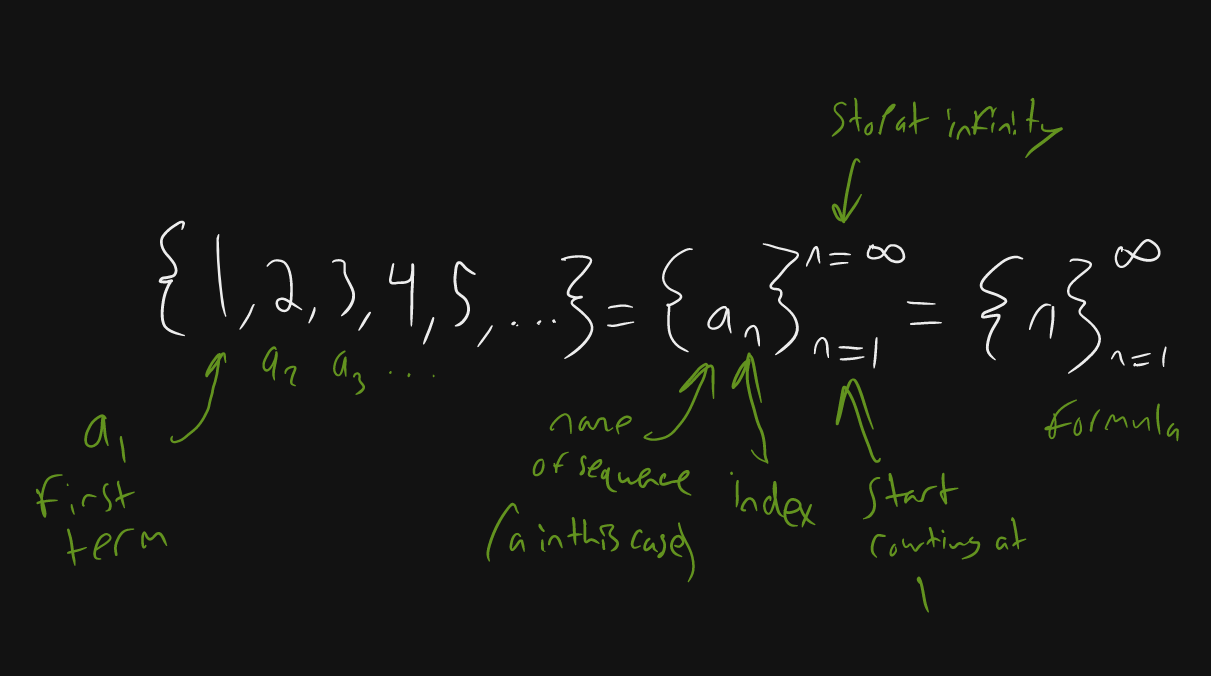
Recurrence Relation §

Another way of writing a formula to generate each term in a sequence. Written using $a_n$ to denote which index you are currently one. For example, $\{1,2,3,4,\mathrm{5...}\}$ can be written as, $a_1=1$ $a_{n+1}=a_n+1$: the n+1th term is one more than the nth term.

Another example $a_1=2$ $\{2,4,6,8,...\}=a_{n+1}+2$

The Fibonacci Sequence can also be written as a recurrence relation $\{1,1,2,3,5,8,13,...\}$ $a_1=1,a_2=1$ $a_{n+2}=a_{n+1}+a_n$

Convergence §

A sequence is said to converge (or is convergent) if ${\lim }_{n\to \infty }{a}_n=L$ exists. The limit is called the Limit of the Sequence.

If ${\lim }_{n\to \infty }{a}_n=DNE$, then the sequence diverges (or is divergent).

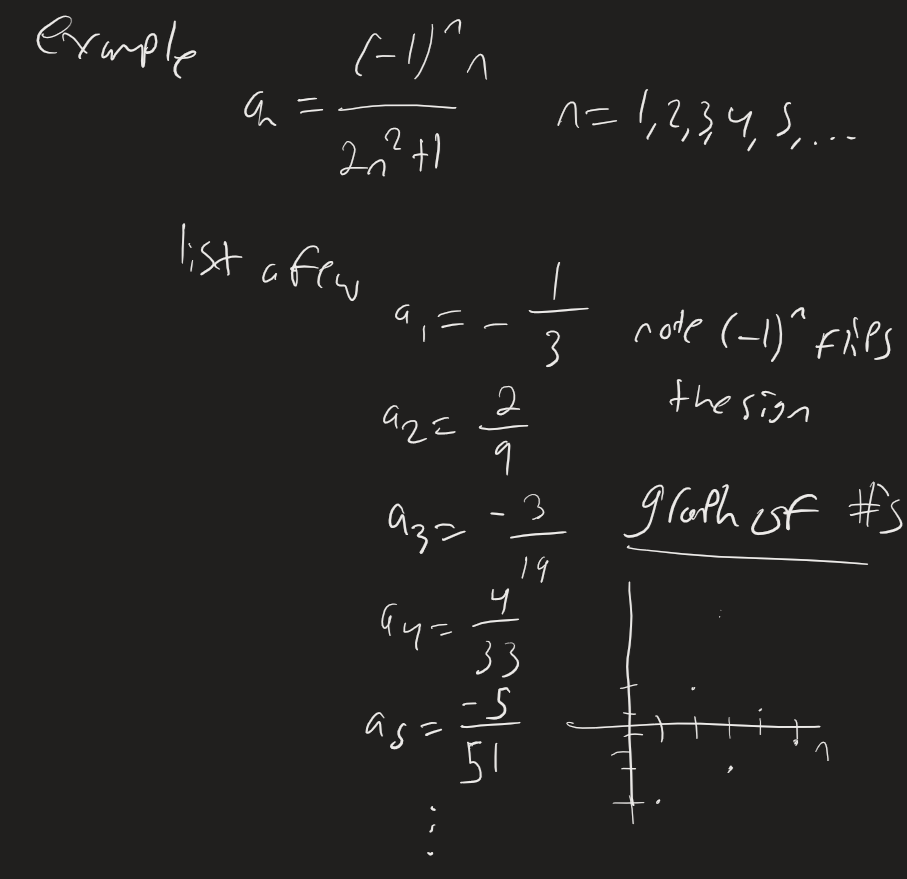The graph and the list suggest that the numbers get closer to zero as n increases. ${\lim }_{n\to \infty }\frac{(-1{)}^{n}n}{n^2+1}=0$ So the limit of this sequence is 0, and therefore the sequence converges.

The limit can be any number.

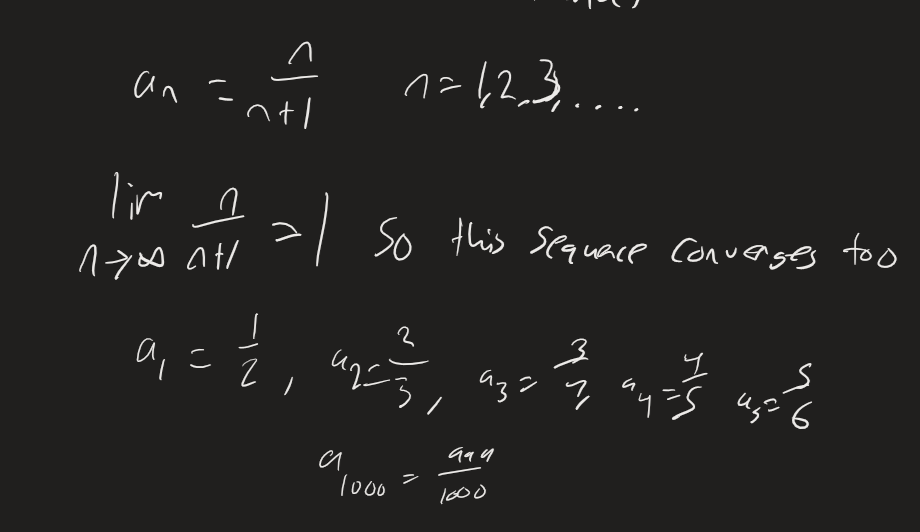
Another example: $\{1,2^{\frac{1}{2}},3^{\frac{1}{3}},4^{\frac{1}{4}},...\}=\{n^{\frac{1}{n}}\}$

$$\underset{n\to \infty }{\lim }{n}^{\frac{1}{n}}=1$$

So the sequence gets closer and closer to 1.

Notice the numbers in that series increase from 1 to 3, but then decrease for everything greater than 3.

Compare this to $\{\frac{n}{n+1}{\}}_{n=1}^{\infty }$ where the terms are always increasing. => This sequence is monotonic, the terms move in one direciton only $\{n^{\frac{1}{n}}\}$ has the terms increasing for a bit then decreasing => It is not monotonic

Both of these sequences are bounded. In $\{\frac{n}{n+1}{\}}_{n=1}^{\infty }$ the terms get no smaller than $\frac{1}{2}$ and no biggre than 1 => It is bounded below by $\frac{1}{2}$ and above by 1 In $\{n^{\frac{1}{n}}\}$ the terms get no smaller than 1 and no bigger than $3^{\frac{1}{2}}$ => It is bounded below by 1 and above by $3^{\frac{1}{3}}$

bounded implies an upper bound and lower bound exist

If a sequence is monotonic and bounded it converges.

Geometric Sequence §

In the geometric series, there is a common ratio $r$ between all succeeding terms.

$\{(\frac{1}{2}{)}^n{\}}_{n=1}^{\infty }=\{\frac{1}{2},\frac{1}{4},\frac{1}{8},...\}$ each term is $\frac{1}{2}$ the term before. §

$\{(\frac{-1}{3}{)}^n{\}}_{n=1}^{\infty }=\{\frac{-1}{3},\frac{1}{9},\frac{-1}{27},...\}$ each term is $\frac{-1}{3}$ the term before. §

The maximum $r$ value for a sequence to converge is 1

The minimum is -1, but it doesn’t converge for -1.

For a geometric sequence to converge, $-1<r\le 1$ or in interval notation (-1, 1]

Growth Rates of Sequences Theorem §

If the denominator of a fraction within a sequence grows faster than the numerator of the sequence, then the sequence converges to 0.