Integrals

#Calc-2#Math#Integrals An Integral is a way of finding the area under a curve between two points on the curve.

To find the area under y=f(x) between x = a and x= b is ${\int }_a^{b}f(x)dx$

• f(x)dx represents the area of a rectangle with length f(x) and width $\Delta x$
• the integral part basically means sum up the areas of all the little rectangles starting at x = a and ending at x = b

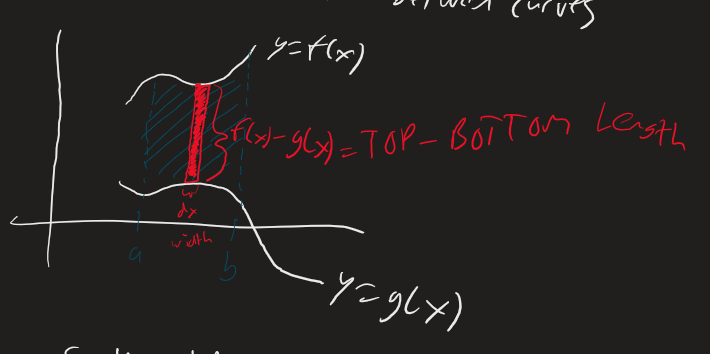
We can extend this definition to get the area of a region between two curves ${\int }_a^b[f(x)-g(x)]dx$ Area of the top curve - area of the bottom

Sometimes it is easier to integrate along the y-axis instead of the x-axis In these cases, convert the functions to be the form x = something y and integrate like normal

When integrating in y, the area between curves becomes right-left

Definite vs Indefinite Integrals §

• A definite integral has numbers, indefinite ones do not
• Definite integrals have a single solution, indefinite ones have infinite
• Definite integrals are evaluated using F(b) - F(a) (Fundamental Theorem of Calculus)
• Indefinite integrals are integrated as per usual and then have a +C added to the end for the constant

Methods of Integration §

Basic Integration Rules §

These are all the basic rules for integrating any kind of integral

Integration by Parts §

Integration by Parts

Integrals involving Trig Functions §

Trig Integrals

Trig Substitution §

Trig Sub

Partial Fractions §

Integration by Partial Fractions

Improper Integrals §

Improper Integrals are a type of integral involving $\infty$ Improper Integral

Applications of Integration §

Integration can be used to find Volumes of Revolution of a graph §

Volumes of Revolution

Integration can be used to find Length of a Curve and Surface Area of a Volume of Revolution §

Surface Area of Volume of Revolution

We can find the length of the curve from a to b with the formula ${\int }_a^b\sqrt{1+[f^{\prime }(x){]}^2}dx$ This formula works as long as f(x) is continuous and differentiable. It works by using the distance formula for very small changes in x and y and then integrating (summing up) all the small segments

Mass of an object with non constant density §

A thin bar that is L meters long, with a constant density has a mass of $m=\rho \ast l$ If the density is NOT constant, we say $\rho (x)$ (greek letter rho(x)), then the mass involves an integration.

Each little slice of the bar would have a mass of $\rho (x)dx$ , and we integrate from 0 to L for the mass of the whole thing $m={\int }_0^L\rho (x)dx$

Linear Spring Force/Work §

Work Formula is Work = Force * Distance, so long as force and distance don’t vary. If either or not constant, then integration is involved.

A spring that has no forces acting on it is at its natural length. The spring has a force that tries to restore itself to equilibrium, for linear springs we model this force with Hooke’s Law: F = k * x

The work done by a spring is $W={\int }_a^b(kx)dx$ where a and b are the starting and ending lengths measured with respect to the springs natural length

Most of these problems involve being given some setup to help you find the k value and then integrating using that k value

Work Against Gravity §

This uses the same work formula, Work = Force * Distance

If a force or distance is not constant in the situation then you have to integrate. An example would be the work needed to wind up a chain.

Pumping Water and Force on a Dam §

Refer to This Notes Page And This ChenFlix