Series

#Calc-2#Math#Series A series is the sum of the numbers in a sequence. A series looks like this 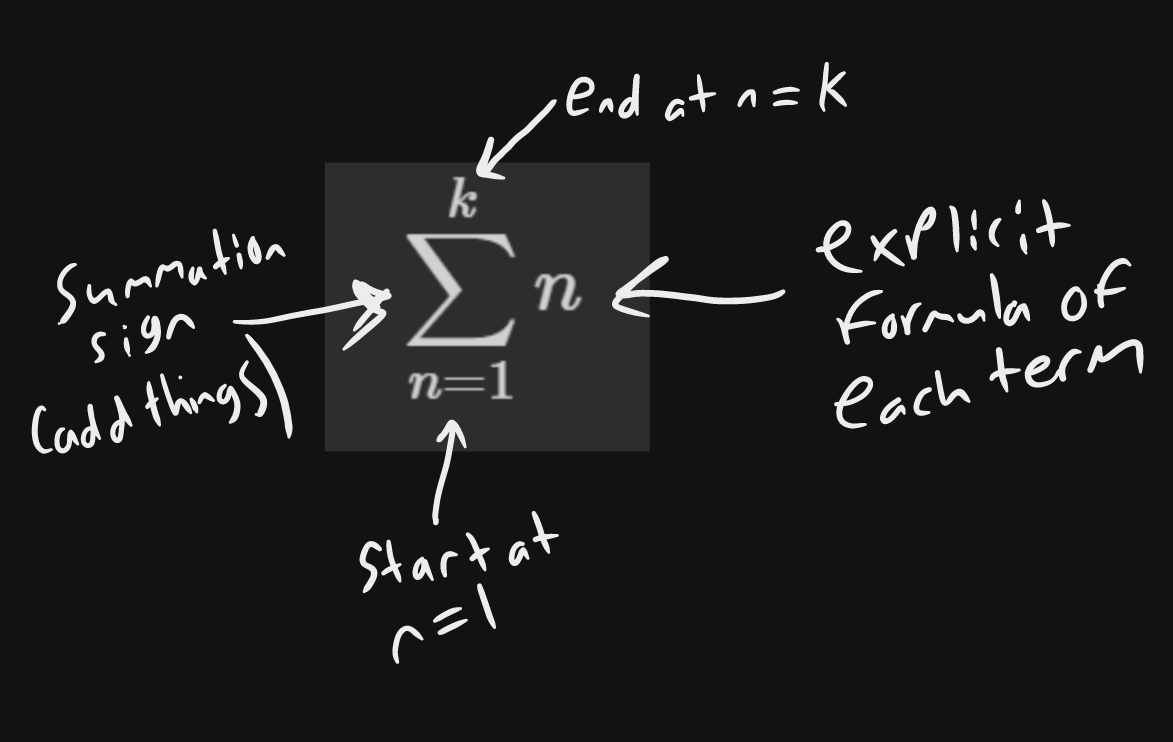Explicit Formula

$\sum _{n=1}^{k}n=1+2+3+4+5+...+k$ This series is finite it ends at a finite $k$ value. §

$\sum _{n=1}^{\infty }n=1+2+3+4+5+...$ This is an infinite series, the series never ends. §

$\sum _{n=1}^{\infty }\frac{1}{2^n}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+...$ §

Partial Sums §

The sum of the first n terms is called the nth partial sum.

Parital sums of $\sum _{n=1}^{\infty }\frac{1}{2^n}$ $S_1=\frac{1}{2}$ - first partial sum $S_2=\frac{3}{4}$ - Sum of the first 2 terms $S_3=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{7}{8}$ $S_4=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{15}{16}$ … $s_{10}=...=\frac{1023}{1024}$ Note the trend: $S_n=\frac{2^{n-1}}{2^n}$ - this is the nth partial sum of the series

The limit as n approaches infinity of $S_n$ exists. ${\lim }_{n\to \infty }\frac{2^{n-1}}{2^n}=1$ This means no matter how many terms are added , the sum will never exceed 1 (the result of the limit above). When the series has a sum we say the series converges or is convergent.

Another way to state it: the series converges if the sequence of its partial sums is convergent. => We want $\{S_1,S_2,S_3,S_4,...\}$ to converge

An example of a divergent series: $\sum _{n=1}^{\infty }cos(n\pi )=-1+1+-1+1+-1+...=\sum _{n=1}^{\infty }(-1{)}^n$ $S_1=-1$ The sequence of partial sums is $\{-1,0,-1,0,-1,....\}$.
$S_2=0$ This sequence has no limit, the partial sums don’t approach $S_3=-1$ a finite number. So this series diverges. $S_4=0$ $S_5=-1$ …

Ways to test if a series converges Convergence Tests §

Types of Series’ §

Geometric Series

Alternating Series

Telescoping Series