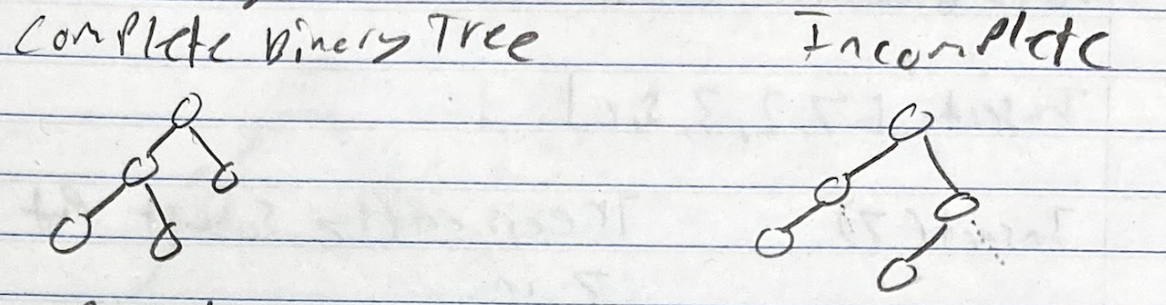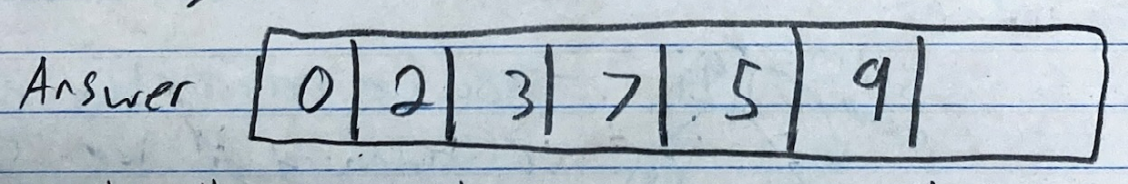Heap

#DataStructure#Computer-Science#CS251

• Heaps use complete Binary Trees in a heap order
  • Complete means all the levels are filled with one exception: the last doesn’t have to be full, but it should be filled in from left to right
    • 
  • Heap Orders
    • Min Heap Order - The key/item of a parent is LESS than its children items
    • 
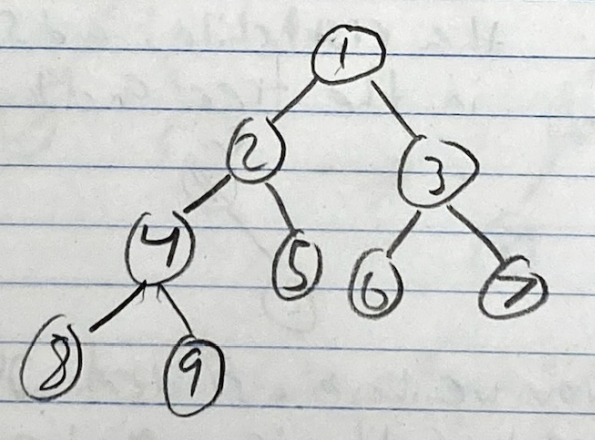
    • Max Heap Order - The keys/items of a parent is GREATER than its children items
    • 
• We visualize and understand Heaps as Trees, but we implement them with Arrays

Methods of a Heap §

• Insert(item)
• Delete(item)
• getMin()/getMax()

Insert(Item) §

Tree Visualization of Insert §

Let’s visualize inserting into a Min-Heap

• Insert [7, 2, 3, 5, 0]
• Insert(7)
  • Tree is empty, so we just put 7 in
  • 
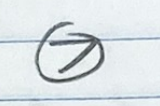
• Insert(2)
  • We insert into the left child first, then the right child, and so on to fill in the tree and keep it’s completeness
  • 
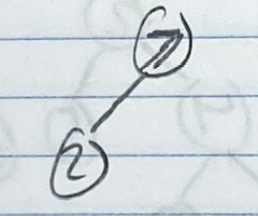
  • Now we have a problem. 2 is in the wrong spot if this is a min heap!
  • We perform a process called Swim Up/Swim Down. If a nodes value is less than it’s parent, it “Swims Up” and swaps with its parent.
  • 
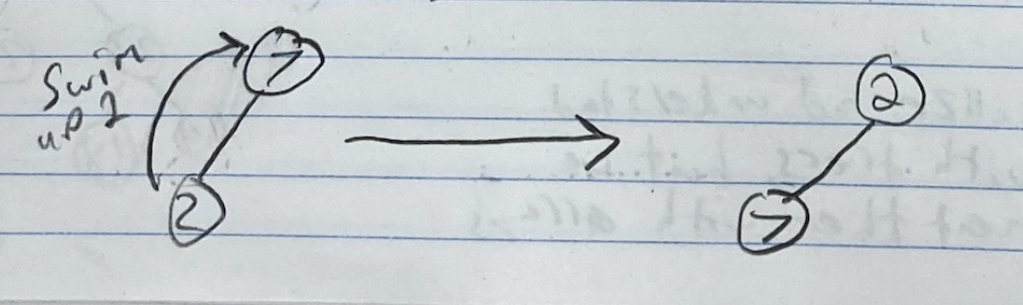
• Insert(3)
  • Now we can insert 3, no problems here
  • 
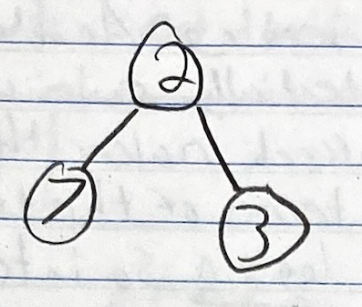
• Insert(5)
  • Next, we insert 5 into the next available slot
  • 
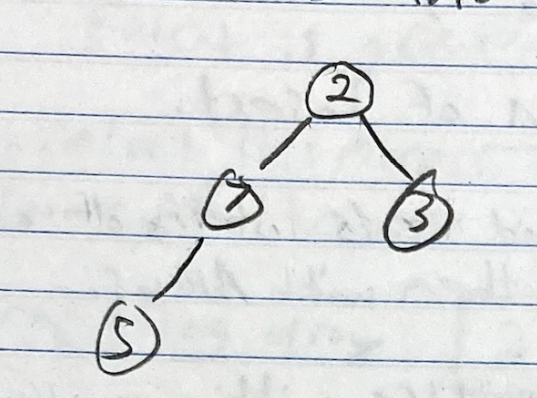
  • It will have to swim up once
  • 
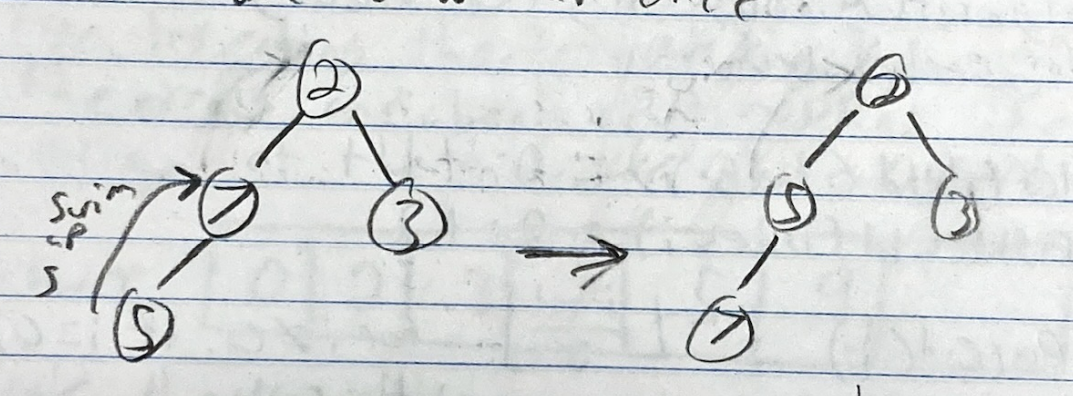
• Insert(0)
  • Again, insert into next available spot, 0 will have to swim up TWICE
  • 
  • This is done by recursively comparing while we swim the node up Notice: We only ever traverse 1 branch of the tree while inserting. A node will be inserted and have to potentially swim up the branch. Only traveling one branch makes this insertion complexity linear in terms of the trees height. The trees height is ${\log }_2(n)$ so in terms of $n$, $\text{Insert(key)}\in O({\log }_{2}n)$

Array Implementation of Insert §

We visualize and understand heaps in terms of a tree, but we actually implement them with arrays.

We can find all the children within an array algorithmicaly using the following formulas for each index:

• leftchild(index i) = 2i+1
• rightchild(index i) = 2i+2
• parent(i) = $\lfloor \frac{i-1}{2}\rfloor$, for $i\ne 0$. if i = 0, we’re at the root

Let’s do the same insertions as before.

• Insert [7,2,3,5,0]
• Insert(7)
  • Start by inserting into the first index
  • 
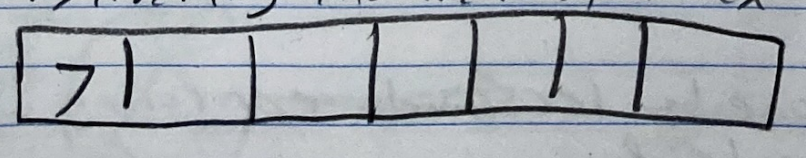
• Insert(2)
  • Again, insert into the next available index
  • 
  • Now check A[1] against A[parent(1)]
    • The parent element is greater, so we have to swim up index 1
  • We repeat this process until there are no more swaps to do OR the index is 0
  • Resulting Array:
  • 
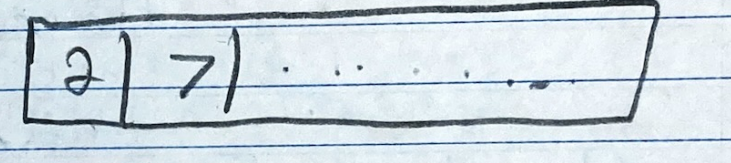
• Try inserting the rest of the values into the array and check if it matches the result array at the end. Keep min heap order!

getMin()/getMax() §

The real power of binary heaps is in the getMin()/getMax() functions. These functions will return the min/max value in the heaps. 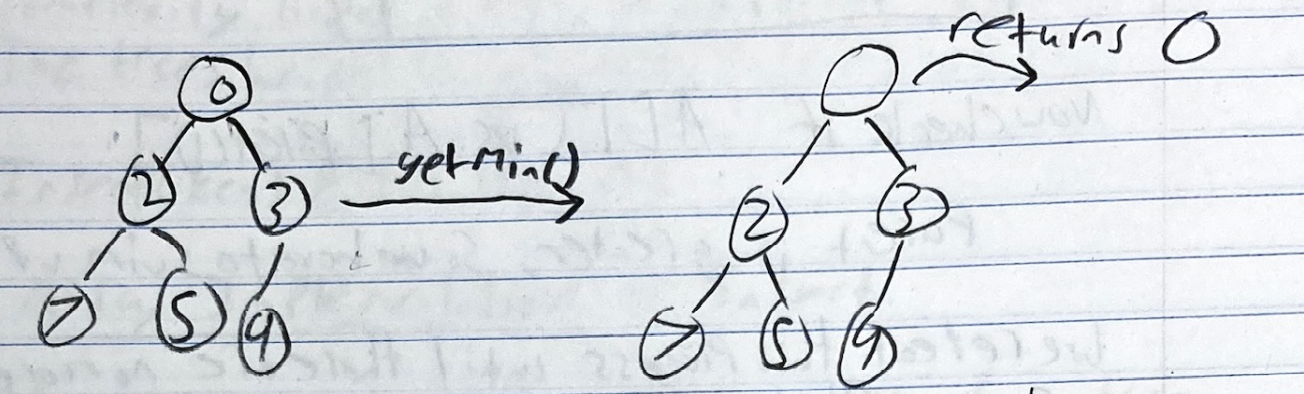When we remove the value at the root, we pick a new number to become the root value.However, we have to keep the completeness of the tree and keep the ordering.

Algorithm to fix the tree §

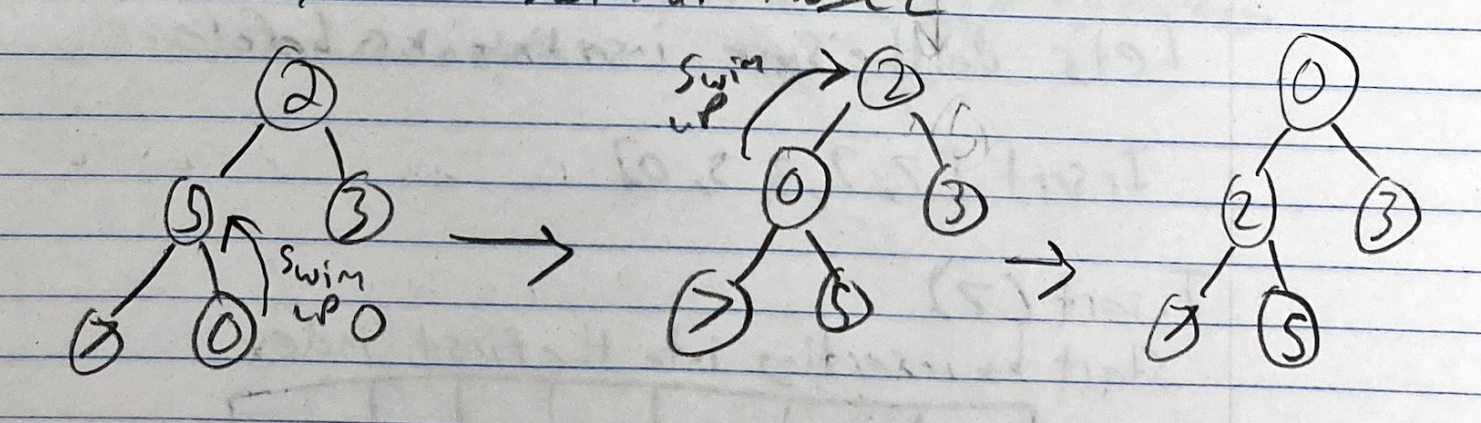
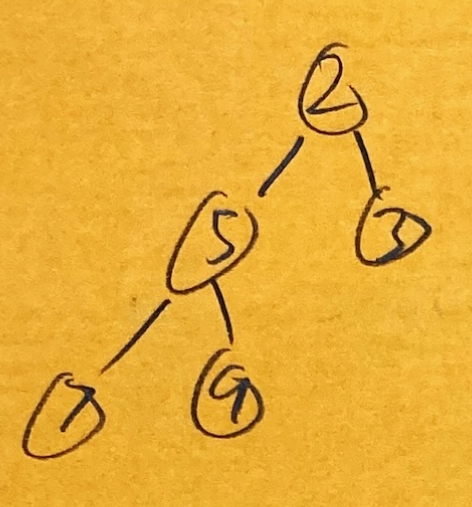
• First, we take the last value of the tree and make it the root value. In this case we use 9
• Now we perform the opposite of swimming up. We “Sink Down” or “Sift Down” until 9 is at the right location. To do this, we swap 9 with the minimum of its children. 2 < 3, so swap 9 and 2.
• 
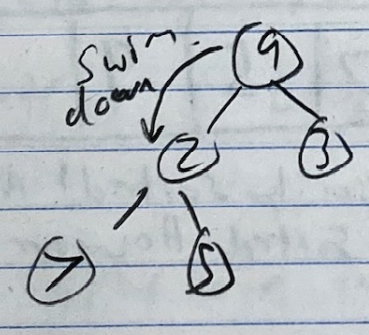
• 9 has to swim down again, because 9 > min{7, 5} and 9 > 5
• 
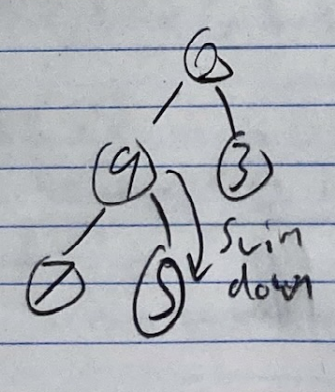
• Now 9 is a leaf (has no children) so we know we’re done
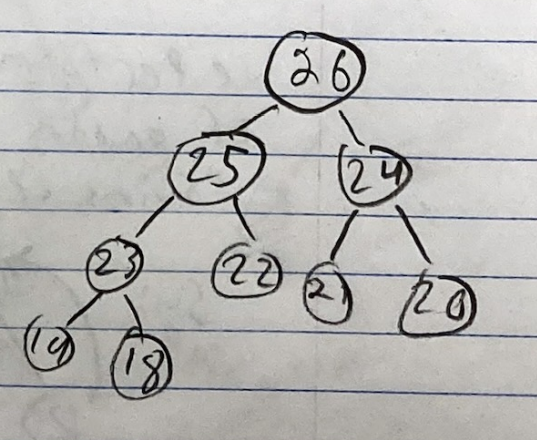
• In a max heap, you check if the parent is less than the max of its children. We only traverse one branch of the tree throughout this process, so $\text{getMin()/getMax()}\in O({\log }_2(n))$

getMin() Array Implementation §

• Return 0 (store it in a temp variable and fix the heap and THEN return it)
• We have to find a new root
• Take the last item, set it as the new root
• 
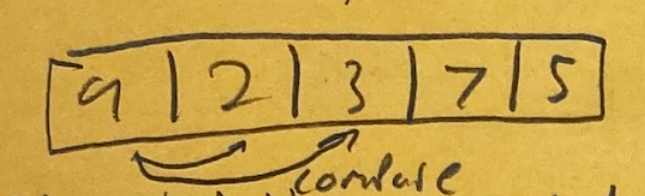
• Now sink down the new root
• A[0] vs min(A[leftchild(0)], A[rightchild(0)])
• We swap, and if it still has children, check again
• After 1 swim down
• 
• After 2nd swim down
• 
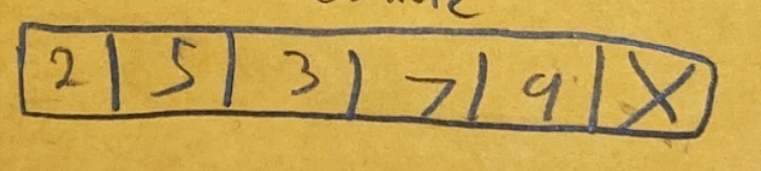
• This process is still $O({\log }_{2}n)$

Summary of Heaps §

Operations:

• Insert(item) $\in O(\log n)$
• getMin()/getMax() $\in O(\log n)$

Heap Order:

• min heap order - each parent is less than its children

• max heap order - each parent is greater than its children

• Heaps are visualized as complete binary trees, however we implement them with arrays

• In the implementations we use the following to find elements within the tree from an index

  • leftchild(index i) = 2i + 1
  • rightchild(i) = 2i + 2
  • parent(i) = $\lfloor \frac{i-1}{2}\rfloor$
    • if i = 0, we’re at the root

• When inserting elements we swim up, comparing inserted elements with their parents to determine whether we need to swap them.

• When getting min/max, we remove the root and put the last element as the new root. Then we swim that element down, comparing it with the min/max of its children and swapping appropriately

Answers §

•