Polar Coordinates

#Calc-2#Math#Polar In Rectangular or Cartesian coordinates, a points location is given by (x, y)

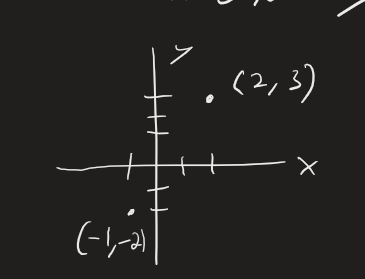
In Polar Coordinates, a points location is given by (r, $\theta$)

• r is the displacement from the origin
• $\theta$ is the angle of a line through the origin and the point in the standard position (with respect to the positive x-axis) Both r and $\theta$ can be negative

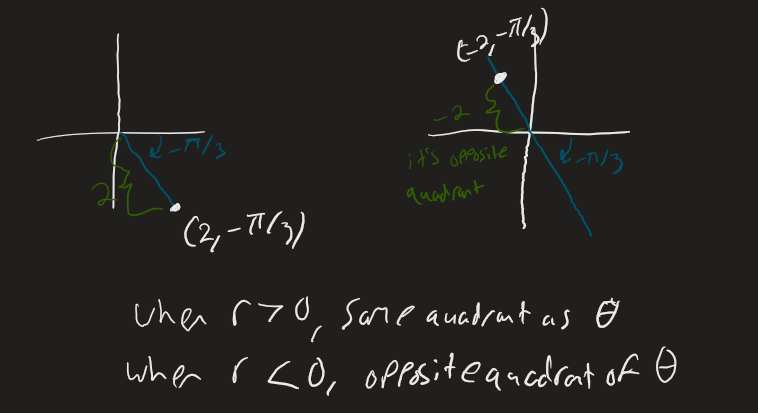
Note that (-2, $\frac{-\pi }{3}$) can also be written as $(2,\frac{2\pi }{3})$ or $(-2,\frac{5\pi }{3})$

Convert from Polar to Cartesian §

(r, $\theta$) -> (x,y) $x=r\cos \theta$ $y=r\sin \theta$ Important to take note of the quadrant, and make sure your coordinates in cartesian will match

Equations can be transformed between coordinate systems as well

$r=3$

• in general, polar equations are in the form of $r(\theta )$
• if any variable is missing, it means that variable can be all values in its domain

in cartesian: $x=r\cos \theta$ $y=r\sin \theta$ $r^2=x^2+y^2$

here $r=3$, so $r^2=9=x^2+y^2\to x^2+y^2=9$ This is the equation of a circle in cartesian!

Polar equations are really good at representing circular type graphs simply Cartesian equations are good at representing straight edge like graphs easily (like lines or squares)

To convert equations, try get there to be rcos$\theta$ or rsin$\theta$ somewhere so you can replace those with x or y respectively.

Convert from Cartesian to Polar (x, y) -> (r, $\theta$) §

We know that $x=r\cos \theta$ $y=r\sin \theta$ $r^2=x^2+y^2$ That final equation also gives us $r=\pm \sqrt{x^2+y^2}$ We also can get theta from x and y, by doing $\frac{y}{x}=\frac{r\sin \theta }{r\cos \theta }=\tan \theta$, ${\tan }^{-1}\left(\frac{y}{x}\right)=\theta$ **make sure the $\theta$ value makes sense with the r we choose => check the quadrant!

Adding $2\pi$ to $\theta$ in a polar coordinate will give the exact same point. In polar there are many ways to represent the same point, in cartesian there’s only one way to represent each point.

When converting equations from cartesian to polar, replace x and y with their respective polar parts and make one side of the equation have all the r’s

Areas and Lengths in Polar Coordinates §

We know how to find the area under a curve in cartesian and the length of a curve.

In polar, these processes get a little more complicated, though the general idea remains the same.

Area under polar curves §

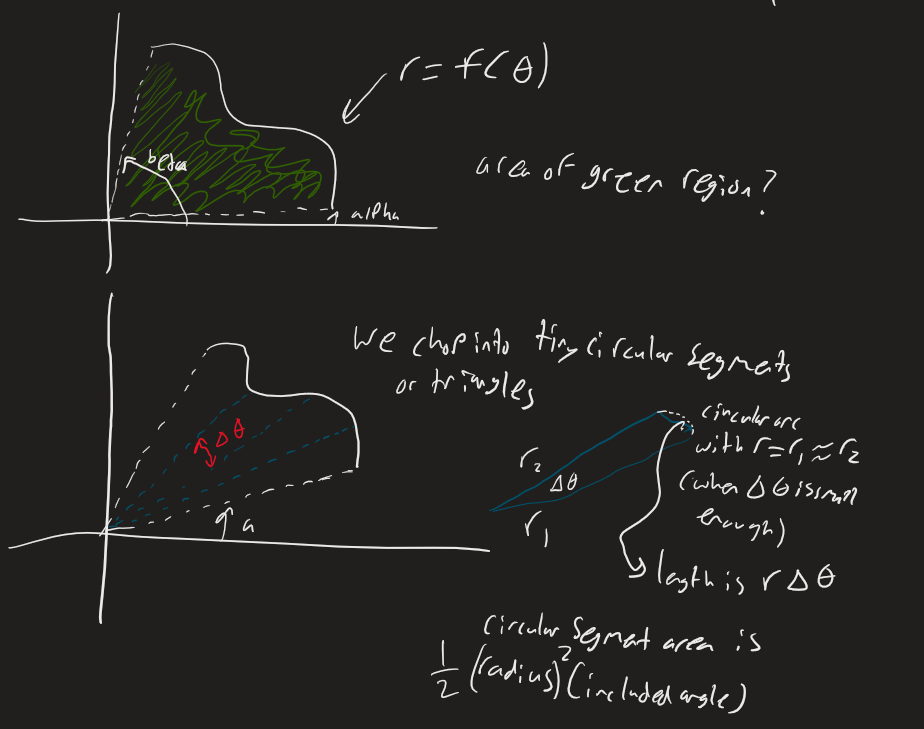
Area of in polar curves: $A={\int }_{\alpha }^{\beta }\frac{1}{2}[f(\theta ){]}^{2}d\theta$

Area between curves $A={\int }_{\alpha }^{\beta }(\frac{1}{2}[outside{]}^2-\frac{1}{2}[inside{]}^2)d\theta$

Length of Polar Curves §

$L={\int }_{\alpha }^{\beta }\sqrt{r^2+{\frac{dr}{d\theta }}^2}d\theta$