Trig Integrals

#Calc-2#Math#Integrals The general idea with more complicated trig integrals is to use some sort of substitution using the basic trig identity ${\sin }^{2}x+{\cos }^{2}x=1$

Strategy for $\int {\sin }^{m}x{\cos }^{n}xdx$ §

Case 1: M or N is positive and odd, the other is any real # (even 0) §

Split off one factor of the thing with the odd power, then rewrite the rest using the basic identity and use substitution

Case 2: M and N are both even and non negative (0 is fine) §

Use the following identities

• ${\cos }^{2}x=\frac{1+\cos (2x)}{2}$
• ${\sin }^{2}x=\frac{1-\cos (2x)}{2}$ and then do substitution

Strategy for $\int {\tan }^{m}x{\sec }^{n}xdx$ §

useful identity for these is ${\tan }^2+1={\sec }^2$, this can be derived from the basic one also helpful to remember that $\frac{d}{dx}(\tan x)={\sec }^{2}x$ and $\frac{d}{dx}(\sec 2)=\sec x\tan x$

Case 1: N is even and positive, M is a real §

split off ${\sec }^{2}x$ to form du, so u can be $\tan x$

Case 2: M is odd and positive, n is a real §

split off $\sec x\tan x$, so u = sec x for du

Trig Substitution §

Consider the integral $\int \frac{1}{\sqrt{1-x^2}}dx$ this cannot be solved via regular substitution

If we consider $\sqrt{1-x^2}$ as one side of a right angle triangle, 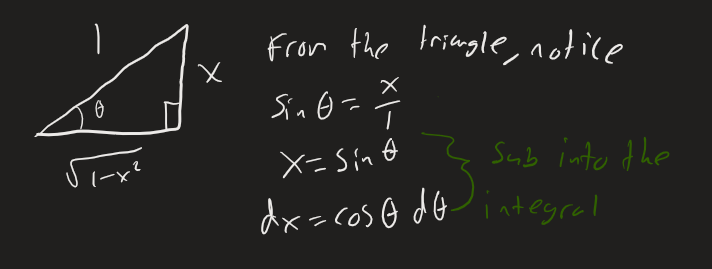Subbing the trig function in,

$\int \frac{1}{\sqrt{1-{\sin }^2\theta }}\cos \theta d\theta =\int d\theta$ $\theta +C$ the original integral was in x, so we have to sub $\theta$ out for x We can find this out by also using the triangle, from the triangle we know that $x=\sin \theta ,\theta ={\sin }^{-1}(x)$

Final answer is ${\sin }^{-1}(x)+C$

The general process §

we form a triangle based on the radical part of f(x) with sides as follows

$\sqrt{x^2\pm a^2},x,a$ The hypotenuse is the square root of sum of squares of the other two sides. Use this to determine which side should be the hypotenuse on your right triangle.

As a general rule of thumb, if there is a constant side we should put it as the adjacent side.

Once you have drawn the triangle, relate x and theta in the simplest way possible using some trig function. Figure out what x and dx should become and sub those into the integral. Solve the integral, likely using a bunch of trig stuff from above. At the end make sure you convert theta back into x. If your integral contains trig functions of theta, you can use the triangle to actually determine the trig function and replace the whole thing instead of just doing a trig function of a trig inverse function.

In definite integrals, you can change the limits to be in terms of theta to make it easier to solve