Hash Tables

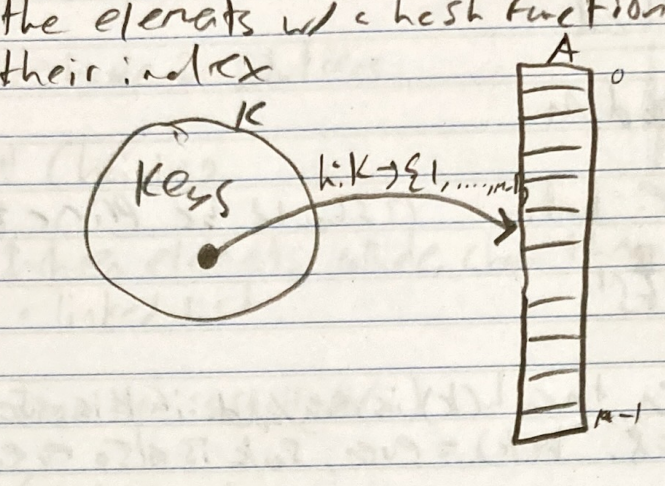
#DataStructure#Computer-Science#CS251 Hash tables map data into an array for faster accessing. This is done via hashing the elements with a hash function to determine their index. Search $\in O(1)$, A[h(k)], key == k Read $\in O(1)$, A[h(k)], key Delete $\in O(1)$ A[h(k)] = null

Hash tables are fast but they definitely aren’t the end all be all. They have their problems

Firstly, they require assumptions about the data.

1. The keys are all unique - this is the optimal situation
2. We replace old values with new values if we use the same key

Hash Table Functions §

• Insert(Key, item data) - insert key with item data
• Get(Key) - get item with key
• Delete(Key) - delete key
• Contains(Key) - does hash table contain key
• isEmpty() - is hash table empty
• Size() - size of hash table
• Keys() - returns array of just the keys

Hash Function §

h is the hash function

h is defined as $h:k\to 0,1,....,m-1$ There are two steps to hashing,

1. prehashing: first we have to transform the key into an integer number
2. map the integer number to an index in $\{0,1,...,m-1\}$

Two Common Hash Functions §

We ignore prehashing, we assume that it has been done already.

Division Method §

$h(k)=k\mathrm{mod}m$

Fairly simple strategy, but, m should be a prime number.

MANY WARNINGS!

1. If m is even, then h(k) is even/odd whenever k is even/odd
   1. e.g., say m=8. h(k) = even, so k must also be even in this scenario
2. if $m=2^p$ then h(k) copies the least p-bits of k
   1. say the key in binary is 0101, and m = 2 (2^1)
   2. hash result copies the least 1 bit from the key, so h(k) = 1 (highlighted bits are the copied bits)
3. if $m=10^p$ then h(k) copies the least p digits of k
   1. key is 1234567890, m= 100 ($10^2$)
   2. h(k) = 90, least 2 digits

Multiplication Method §

$h(k)=\lfloor m(k\cdot A\mathrm{mod}1)\rfloor$ $A$ is a number between 0 and 1 A common value for $A$ is $\frac{\sqrt{5}-1}{2}=\mathrm{0.6180...}$, which is close the golden ratio

Issue: Collisions §

What happens when two keys are hashed to the same index? This is called a collision

We have 2 solutions to collisions.

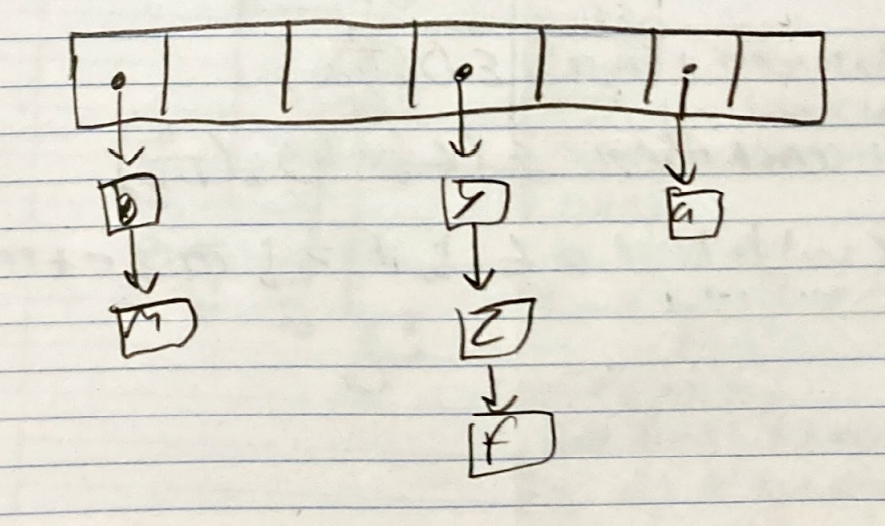
Chaining §

When elements collide, chain them together into a linked list

Insertion is still $\in \Theta (n)$

Searching however changes

• The absolute worst case is $\in O(n)$
• We look at the load factor to get a true time complexity
  • $\alpha =\text{load factor}$
  • $\alpha =\frac{n}{m}=\frac{\text{number of items}}{\text{capacity}}$
  • $O(1+\alpha )$ is more accurate
• We want to keep $\alpha \le 2$, if $\alpha >2$, resize the table and re hash every element

Open Addressing §

Find another available slot for the element when two elements collide

• The load factor will always be $0<\alpha <1$
• There are 3 ways to find an open index
  • Linear Probing - $h(k,i)=(h^{\prime }(k)+i)\mathrm{mod}m$
  • Quadratic Probing - $h(k,i)=(h^{\prime }(k)+C_1+C_2\cdot i^2)\mathrm{mod}m$
  • Double Hashing - $h(k,i)=(h_1(k)+i\cdot h_2(k))\mathrm{mod}m$

WARNING With open addressing, we NEVER want to fully delete things. Instead, replace deleted items with a dummy object.

Analysis §

• An unsuccessful search $\in O(\frac{1}{1\cdot \alpha })$
• A successful search $\in O(\frac{1}{\alpha }\cdot {\log }_2(\frac{1}{2\cdot k}))$ We want to keep $\alpha \le .5$ if $>.5$ resize and rehash