3D Vectors and Shapes

#Calc-2#Math#Vectors

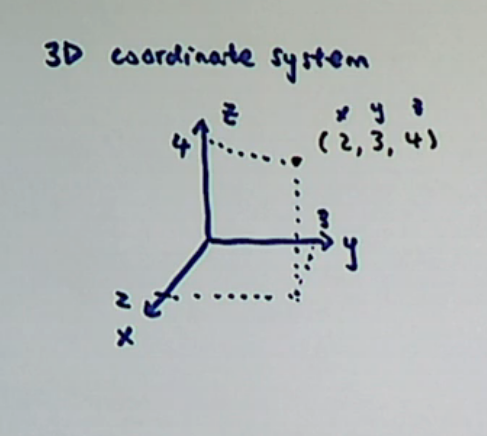
3D Coordinate System §

theoretically adding more dimensions looks the same, we just can’t draw them

3D Vectors §

Everything we have learned about Vectors already transfers over

Vectors in 3d are basically the same, they just have a third number for the z direction

$<a,b,c>$ a - x direction b - y direction c - z direction

Find magnitude the same way, just $\sqrt{a^2+b^2+c^2}$

Everything is the same as two dimensional vectors, just with an extra number

Vector from P(1, 2, 3) to Q(4, 6, 8) $\overrightarrow{PQ}=<3,4,5>$ $|\overrightarrow{PQ}|=\sqrt{3^2+4^2+5^2}=\sqrt{50}$ Subtract destination from starting

Unit Vectors in 3D are the same §

The general unit vectors are

• $\vec{i}=<1,0,0>$
• $\vec{j}=<0,1,0$
• $\vec{k}=<0,0,1>$

Unit Vectors

Operations are the exact same §

$<1,2,3>+<4,5,6>=<5,7,9>=5\vec{i}+7\vec{j}+9\vec{k}$ $\vec{i}$ is the unit vector in the x direction $\vec{j}$ is unit vector in y direction $\vec{k}$ is unit vector in the z direction

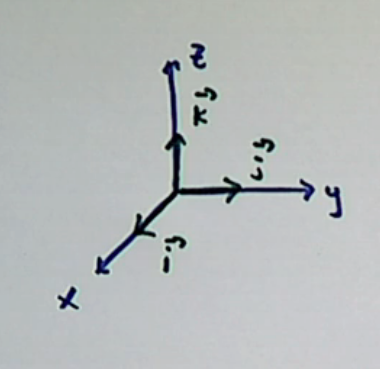
Both Dot Product and Cross Product are the exact same

Basic Shapes in 3D §

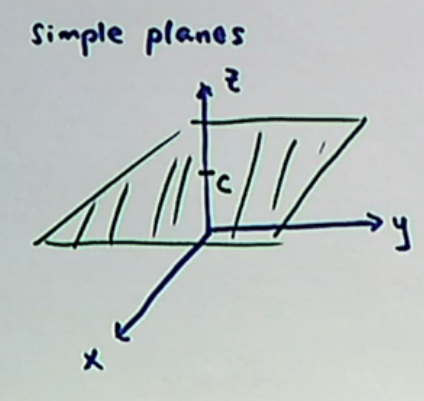
Planes §

A Plane parallel to the xy-plane going through z=c is written as z=c similarly, x=a is a plane parallel to the yz-plane, through x=a

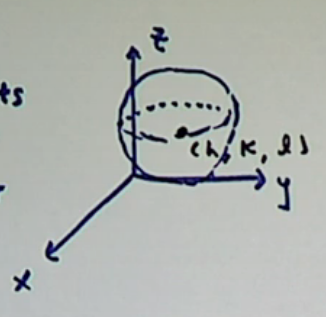
Sphere §

Center of the sphere (h, k, l)

A sphere is the set of all points at distance r from the center

distance formula: $r=\sqrt{(x-h{)}^2+(y-k{)}^2+(z-l{)}^2}$

$(x-h{)}^2+(y-k{)}^2+(z-l{)}^2=r^2$ The standard form of equation of a sphere centered at (h, k, l), with a radius r

If the equation is not in standard form how do we find the center and radius?

$x^2+y^2-z^2-14x+12y+25=0$ To get into standard form, complete the squares

$x^2-14x+y^2+12y+z^2=-25$ ^ ^ Add to both sides the square of half of the numbers marked

$x^2-14x+(-7{)}^2+y^2+12y+(6{)}^2+z^2=-25+(-7{)}^2+(6{)}^2$ $(x^2-14x+49)+(y^2+12y+36)+(z^2)=60$ $(x-7{)}^2+(y+6{)}^2+z^2=60$ center of this sphere is (7, -6, 0) and the radius is $\sqrt{60}$

Examples with Vectors in Three Dimensions §

Vectors Pictured $\overrightarrow{AE}=<-2,0,-4>$ $\overrightarrow{BE}=<0,-2,-4>$ $\overrightarrow{CE}=<2,0,-4>$ $\overrightarrow{DE}=<0,2,-4>$ These cables are all symmetric

Due to symmetry, we know all four cables have to supply the same force

The force along cable $AE$ is $x\overrightarrow{AE}$ where x is some unknown number The force along each cable is x times the vector $x\overrightarrow{BE}$ $x\overrightarrow{CE}$ $x\overrightarrow{DE}$

All we have to do is find x, then the magnitude of $|x\overrightarrow{AE}|$ is the force on that cable

The force exerted by the block is $-500\vec{k}=<0,0,-500>$ The situation is in equilibrium, nothing is moving or changing, which means the sum of the forces from the cables must be equal to the block force

$x\overrightarrow{AE}+x\overrightarrow{BE}+x\overrightarrow{CE}+x\overrightarrow{DE}=<0,0,-500>$ $x<-2,0,-4>+x<0,-2,-4>+x<2,0,-4>+x<0,2,-4>=<0,0,-500>$ $x<0,0,-16>=<0,0,-500>$ $-16x=-500$ $x=\frac{500}{16}=\frac{125}{4}$

So, the force supplied by cable $AE$ is $|x\overrightarrow{AE}|=|<\frac{125}{4},0,-125>|\approx 140$ lb

Each cable supplies 140 lbs of force to hold up the block.