2-3 Tree

#Computer-Science#CS251#DataStructure 2-3 Trees are always balanced, solving our problem from above. There are two types of nodes in a 2-3 tree.

• A 2-node has one item, and two children.
  • 
  • The item I is less than the right child and greater than the left child ($\text{left}<I<\text{right}$)
• A 3-node has two items and three children.
  • 
  • The left child is less than $I_1$, and the right child is greater than $I_2$. The middle child is in between $I_1$ and $I_2$
  • $\text{left}<I_1<\text{middle}<I_2<\text{right}$

Inserting on a 2-3 Tree §

1. Move down the tree going right or left or down the middle as needed until you reach a leaf.
2. Transform that leaf
   1. A 2-node becomes a 3-node
   2. A 3-node becomes a 4-node
      1. A 4-node is split. The middle item get’s pushed up the tree.
      2. 

Try inserting 1, 2, 3, 4, 5, 6, 7, 8 on a 2-3 tree. 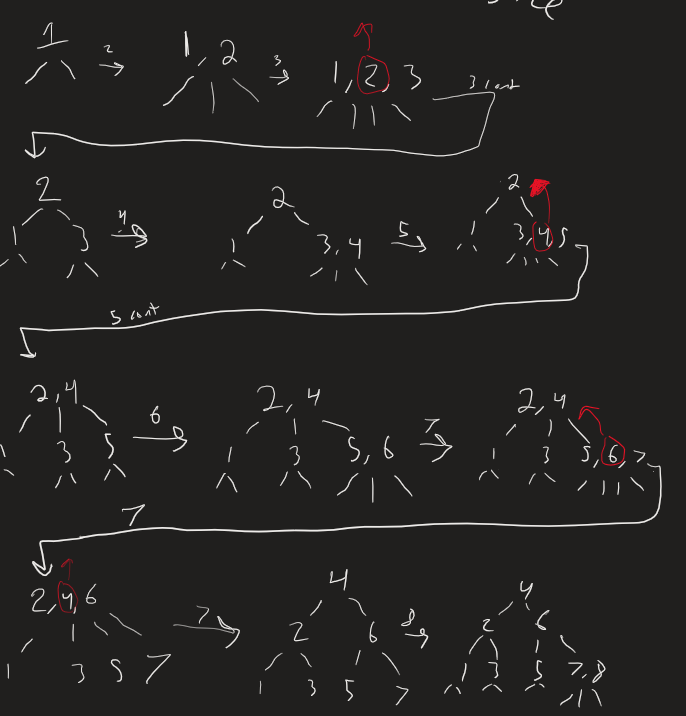It stays balanced, unlike the Binary Search Tree.

Height §

• If a tree is made up of all 2-nodes, then the height of the tree $h\in O({\log }_{2}n)$
• If a tree is made up of all 3-nodes, then the height of the tree $h\in O({\log }_{3}n)$

Search §

Searching on a 2-3 tree is basically the same as a binary search tree. On a 2-node you do the exact same thing. If less than the item go left, if greater than it go right. On a 3-node check if the item is less than $I_1$, greater than $I_2$ , or if both of those are false, then go down the middle child.

Search is $\in O(\log n)$

For search trees in general, deleting is never very straightforward. There are often many cases to consider. Here’s an example of deleting a tree. 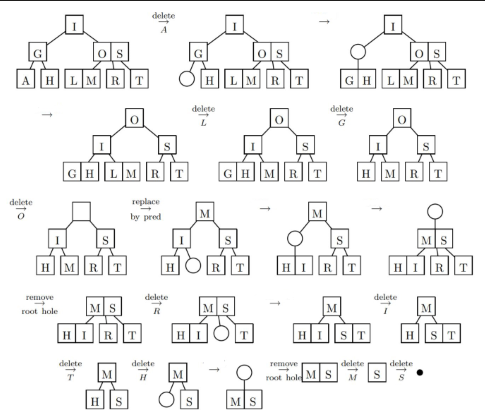Whatever transformations are applied, you have to maintain a balanced and valid 2-3 tree.