Quick Sort

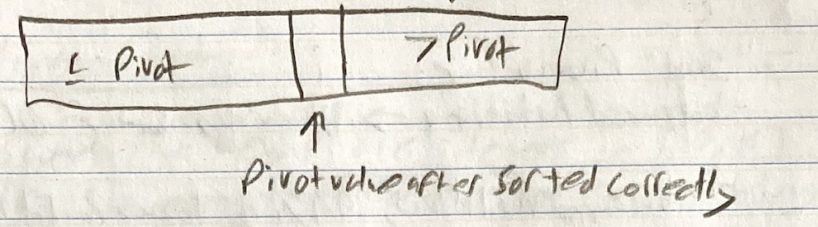
#CS251#Computer-Science#Sorting We pick a pivot value from the array, put it into its right position, then call QuickSort on the other two halves of the array

Pseudocode §

QuickSort(A: array, l: left boundary, r: right boundary)
	if (l < r)
		m <- Partition(A, l, r) // returns index for pivot value
		QuickSort(A, l, m-1)
		QuickSort(A, m+1, r)
	end if
	return A
end QuickSort

Partition(A, l, r)
	p <- A[r], i <- l-1
	for (j = l to r-1)
		if (A[j] < p)
			i <= i+1
			swap(A, i, j)
		endif
	endfor
	i+=1
	swap(A, i, r)
	return i
end Partition	

Analysis §

Things can go right here and things can go wrong

• What can go right?
  • We get a “good” pivot value
    • This can create balanced partitions, we end up like Merge Sort $\in O(n\log n)$
    • This could also create unbalanced partitions, where 99% of the items go to one partition and 1% goes to the other partition. Even in this extreme cdase, QuickSort is still $O(n\log n)$
• Worst Case
  • We choose the worst pivot value (the maximum value as the pivot)
    • This creates one partition with the remaining items and one with no items
    • This time complexity ends up being $\in O(n^2)$