- Anytime you are working with a financial goal that involves money, time, and interest, you will want to use TVM calculations
- Every TVM calculation involves 5 inputs
-The Future Value — the amount of money you expect to have at the end of the goal timeline.
- The Present Value — the amount of money you have at the beginning of the goal timeline or presently.
- The Number of Periods in your goal timeline.
- The Interest Rate you expect to earn on your savings.
- And the Payment which can either be money saved or money spent during the goal timeline.
- If your savings or spending payments are equal for every period it’s called an annuity and its the type of TVM calculation we care about the most
Note
Most financial calculators assume that payments get deposited or spent at the END of a period. If a payment is due at the beginning of the period its called an “annuity due” and requires an additional step in the calculation. All these examples assume (unless stated otherwise) that payments are at the end of the period.
- Drawing a timeline is the easiest way to visualize any time value of money problem
- Remember you always need 4 of the 5 inputs at least so you can identify which one to solve for
- It is often easiest to use a calculator for these problems Financial Calculators
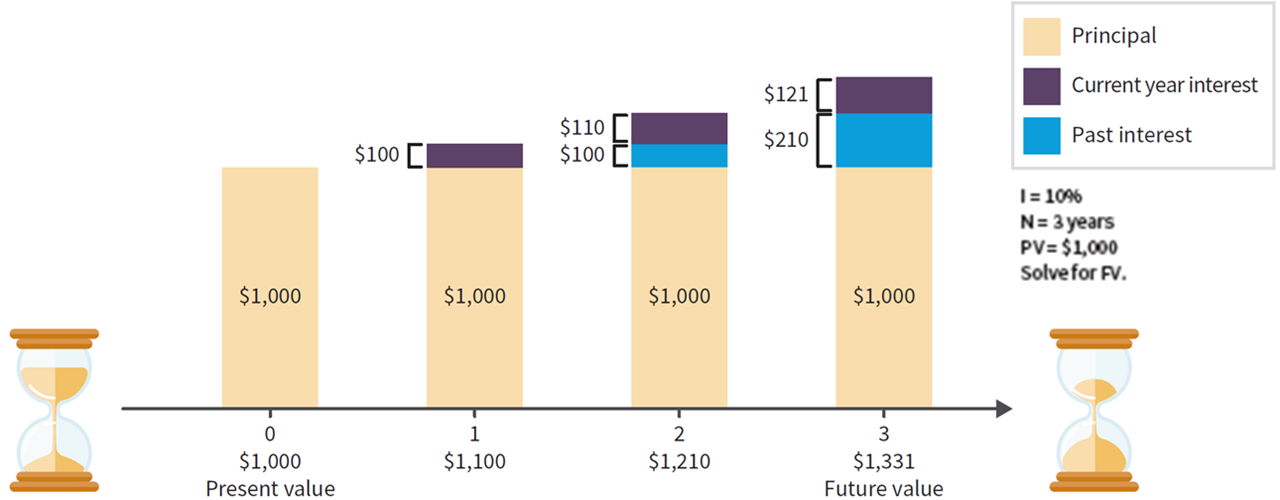
- Example 1
- If you start with $1000 today how much will you have in 3 years if you can earn 10% each year?
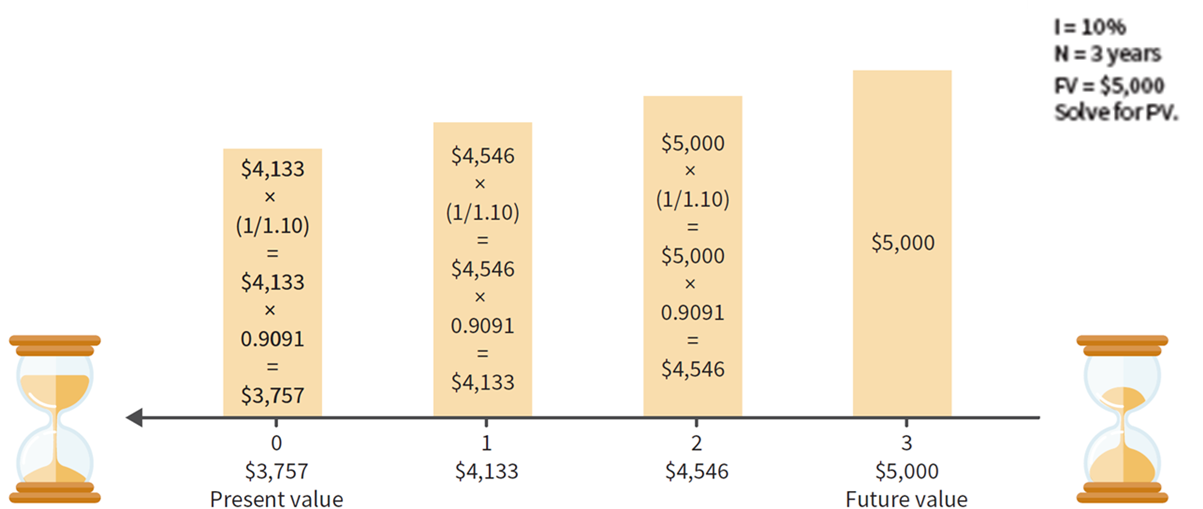
- You can also work backwards with the same process. How much do you need today (present value) if you know you will need $5000 in 3 years earning 10% interest?
- The Rule of 72
- To find the approximate number of years or periods needed to double your money, dive 72 by the interest rate
- How many years will it take to grow 3000 to 6000 earning 3% interest?
- 72/3 = 24 years
- To estimate the approximate interest rate needed to double your money, divide 72 by the number of years (or periods) in your goal time horizon
- What interest rate will turn 3000 into 6000 over 6 years?
- 72/6 = 12%
- This is only a rough estimation, it is never going to be accurate
- Remember that for every Time Value of Money scenario, there are five total inputs:
- N — the number of compounding time periods;
- I — your interest rate;
- Present Value — how much you have now;
- Payments — regular withdrawals or deposits during the time period, and
- Future Value — how much you will have after N time periods.
- Example 2
- Let’s say that you receive $1000 at graduation. If you invest the gift and earn 8% annually, how much will you have in 20 years?
- N = 20 (number years)
- I/Y = 8 (interest per year not converted to a decimal, just the percent)
- PV = (-) 1000 (present value, must always be entered as negative or else you get an error)
- PMT = 0 (payments, no additional payments made in this problem)
- CPT FV = 4,660.9571 (future value, this is the answer we get from the calculator not from the problem)
- Example 3
- You are offered the choice of taking 1000 today or 1200 in 5 years. You can earn 5% interest
- For this problem, we want to see the initial value we would need to invest to get 1200 in 5 years. If it ends up less than 1000, we would be better off investing the 1000 today then getting 1200 later, since after 5 years you would have more than 1200.
- Alternatively you could find the future value form investing 1000 today and see if its more than 1200.
- N=5
- I/Y=5
- CPT PV = (-) 940.2314 < $1000, take the 1000 today
- PMT = 0
- FV = 1200
- Example 4 (Future value of an annuity)
- How much will you accumulate in 20 years if you start saving 1000 every year and earn 9% savings
- N= 20
- I/Y = 9
- PV = 0
- PMT = (-)1000
- CPT FV = 51,150.1196
- Example 5 (Present value of annuity)
- Imagine that you have just received a sizable inheritance with the following choice: (1) take a lump sum of 1 million dollars today or (2) receive 75000 per year for the next 20 years. The interest rate is 5%
- N= 20
- I/Y = 5
- CPT PV = (-) 934,665.7757 < 1 million so take the 1 million lump sum
- PMT = 75000
- FV = 0
- Example 6 (Amortized payment)
- An amortized payment is a payment of the same amount for a set number of months or years, such as for paying off a car loan
- Say that max wants to borrow 250,000 to purchase a home. He can get a 30 year loan at a 6% interest rate. Compute Max’s monthly payment amount
- N = 360 <- 30 years times 12 months
- I/Y = 0.5 <- 6% annual interest rate / 12 months
- PV = 250,000
- CPT PMT = (-) 1,498.8763
- FV = 0 <- because the loan will be paid off