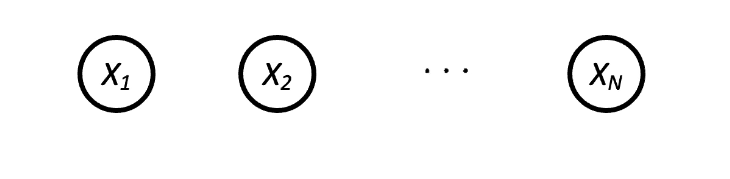Bayesian Networks

Probabilistic Models §

• Models describe hos (a portion oif) the world works
• Models are always simplifications
  • They may not account for every variable
  • May not account for all interactions between variables
  • “All models are wrong; but some are useful” - George E P Box
• What do we do with probabilistic models?
  • We (or our agents) need to reason about unknown variables, given evidence
  • Example: explanation (diagnostic reasoning)
  • Example: prediction (causal reasoning)
  • Example: value of information

Bayesian Networks §

• Two problems with using full joint distribution tables:
  • Unless there are only a few variables, the joint distirbution is WAY too big to represent explicitly
  • Hard to learn empirically about more than a few variables at a time
• Bayesian networks: a technique for describing complex joint distributions (models) using simple, local distributions (conditional probabilities)
  • A special case of graphical modles
  • Describe how variables locallyi interadct
  • Local intercations chain together to give global indirect actions

Graphical Model Notation §

• Nodes: random variables (with domains)
  • Can be assigned (observed) or unassigned (unobserved)
• Edges: interactions
  • Indicate “direct influence” between variables
  • Formally: encode conditional independence
  • Imagine that arrows mean “direct causation” (in general they do not, but this is a convenient assumption for now!)
• Example: N independent coin flips
  • 
  • No interactions between variables: absolute independence
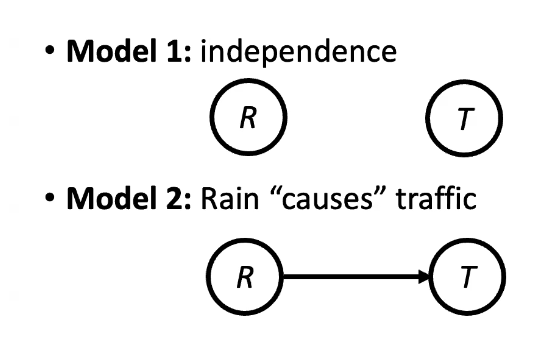
• Example: Traffic
  • Variables
    • R: It rains; T: there is traffic
  • Model 1: indpendence
  • Model 2: Rain “causes” traffic
  • 

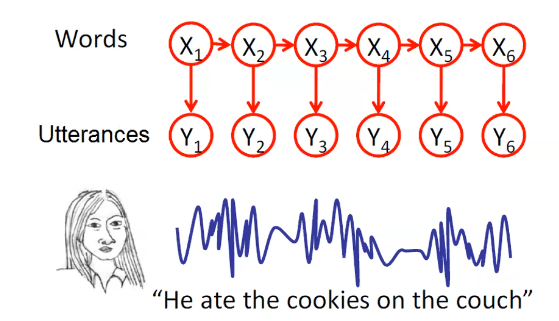
Real world Application: Speech recognition §

• Infer spoken words from audio signals
• Markov Assumption: the future and past are indpendent given the present
• Hidden variable $X_i$ (words)
• Observed variable $Y_j$ (waveform)
• Goal: Infer $P(X_i|Y_1,\dots ,Y_n)\forall i$
• 

Bayesian Network (BN) Semantics §

• A set of notdes, one per random variable X
• A directed, acyclic graph
• A conditional distribution for each node
  • A collection of probability distributions over X, one for each combination of parents’ values
  • $P(X|a_1,\dots ,a_n)$
  • CPT: conditional probability table
  • Description of a noisy “causal” process

Probabilities in BNs §

• Bayes’ nets implicitly encode the joint distribution as a product of local conditional distributions:
• $P(x_1,x_2,\dots x_n)=\prod _{i=1}^{n}P(x_i|parents(X_i))$
• To see what probability a BN gives to a full assignment, multiply all the relevant conditionals together
• Why are we guaranteed that BN results in a proper joint distribution?
• Chain rule (valid for all distributions): $P(x_1,x_2\dots x_n)=\prod _{i=1}^{n}P(x_i|x_1\dots x_{i-1})$
• Combining this with an assumption of conditional indpendence makes a proper joint distribution
• A BN cannot represent all possible joint distributions
  • The topology enforces certain conditional indepdnencies