Logic and Reasoning

Knowledge Base §

• Knowledge Base (KB) is a set of sentences in a formal language
• TELL the Agent what it needs to know
• The agent can then ASK itself what to do
• The answers should follow from the KB
• $\forall xBird(x)\to Fly(x)$
  • For all objects that exist in the world, if the object is a bird, then the object can fly
  • …Penguins exist. They can’t fly! We have to be careful when constructing the Knowledge Base!
• Agents are only as smart as their knowledge base
• In this course (CS 471) we focus on Propositional logic and languages rather than natural language (english)

The wumpus world: task environment characteristics §

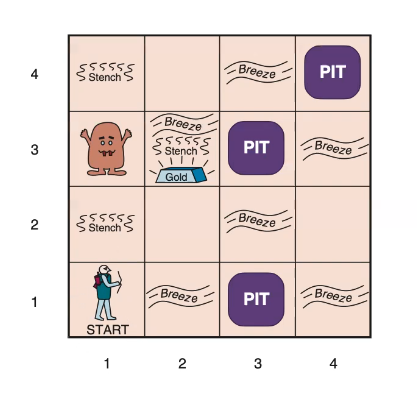
• Performance Measure
  • Gold +1000, Death: -1000, -1 per step, -10 for using arrow
• Environment
  • Squares adjacent to wumpus are smelly
  • Squares adjacent to pit are breezy
  • Glitter iff gold is in the same square
  • Shooting killswumpus if you are facing it; shooting uses up the only arrow
  • Grabbing picks up gold if in same square
• Actuators:
  • Left turn, right turn, forward, grab shoot
• Sensors:
  • Breeze glitter smell We as humans can reason about this environment and the rules, even if we didn’t have all the information. For example, if we were in a square with stench, we’d know Wumpus is in one of the adjacent squares. If we go to square (1, 2) for example, Wumpus must be in (1,3) or (2,2). Then we could go down and to the right to (2,1). We’d notice a breeze. So either (3,1) or (2,2) is a pit. However, as humans we can see the connection that since there was no breeze in (1,2), (2,2) cannot be a pit. We also see that since (2,1) is not smelly, Wumpus cannot be in (2,2) so now we know that (2,2) is actually safe.
    The question then is, how do we translate this logic and thinking to our Search Agents when they operate in partially observable environments like this one?

Entailment §

• Entailment means one thing follows from another
• $KB\models \alpha$
• Knowledge base KB entails sentence $\alpha$ if and only if $\alpha$ is true in ALL WORLDS where KB is true
  • “I am hungry” entails “Either I am hungry or I am thirsty”
  • “There is no breeze here” entails “There is no pit in an adjacent square”
  • $(x+y=4)\models (4=x+y)$
• Models are formally structured possible worlds with respect to which truth can be evaluated
• A sentence $\alpha$ is true in model $m$:
  • $m$ is a model of $\alpha$
  • $m$ satisfies $\alpha$
• Entailment $KB\models \alpha$ iff $M(KB)\underline{\subset }M(\alpha )$
• Important: $M(\alpha )$ = set of all models of alpha
• Every world where KB is true, alpha is also true

Inference §

• Inference: procedure\algorithm to derive consusions
• $KB{⊢}_i\alpha$: setence alpha can be derived from KB by prcoedure i
• Soundness: i is sound if whenever KB derives alpha it is true that $KB\models \alpha$
• Completeness: i is complete if whenever KB models al;pha, it is also true that KB derives alpha via procedure i

Propositional Logic: Syntax §

• Atomic sentences
  • Proposition symbols: A proposition that can be true or false
  • Always true proposition or always false proposition: True, False
• Complex sentences:
  • If S is a sentence $\neg S$ is a sentence (negation)
  • If S1 and S2 are sentences, $S1\wedge S2$ is a sentence (conjunction, AND)
  • If S1 and S2 are sentences, $S1\vee S2$ is a sentence (disjunction, OR)
  • If S1 and S2 are sentences, $S1\oplus S2$ is a sentence (exclusive disjunction, EXCLUSIVE OR, XOR)
    • S1 or S2 is true but not both
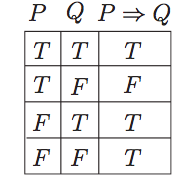
  • If S1 and S2 are sentences, $S1\to S2$ is a sentence (implication, S1 implies S2)
    • S1 is false or S2 is true (is false iff S1 is true and S2 is false)
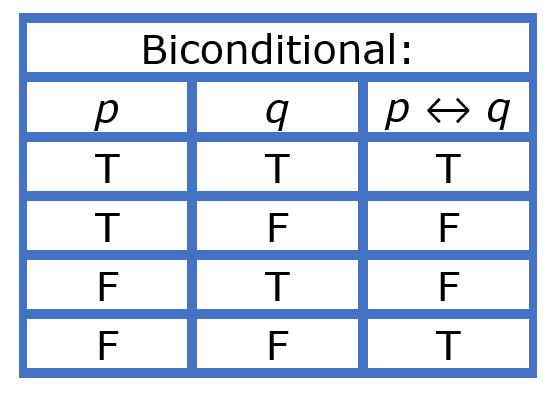
  • If S1 and S2 are sentences, $S1\leftrightarrow S2$ is a sentence (biconditional, IFF)
  • 
  • 
  • 

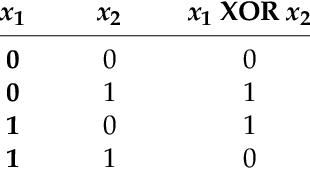
How to determine entailment? §

Two methods

• Theorem proving: Application of inference rules
  • Legitimate (sound) generation of new sentences from old
  • Proof = a sequence of inference rule applications
    • Can use inference rules as operators in a standard search algorithm
  • Typically require transformation of sentences into a normal form
• Model checking
  • Truth Table enumeration (always exponential in n)
  • Improved backtracking, eg. Davis Putnam Logemann Loveland (DPLL)
  • Heuristic search in model space (sound but incomplete) e.g. min-conflicts-like hill-climbing algorithms

Theorem Proving §

We need to know if two sentences are logically equivalent for this.

• Two sentences are logically equivalent if and only if they are true in the same set of models: $\alpha \equiv \beta$ iff $\alpha \models \beta$ and $\beta \models \alpha$
• A sentence is valid if it is true in ALL models
• A sentence is satisfiable if it is true in SOME models
• A sentence is unsatisfiable if it is true in NO models ($A\wedge \neg A$)
• Validity is connected to inference via the Deduction Theorem:
  • $\alpha \models \beta$ if and only if $\alpha \to \beta$ is valid
• Satisfiability is connected to inference via the following
  • $\neg (\alpha \to \beta )$ is true for NO model
  • simplifies to $\alpha \wedge \neg \beta$
  • $\alpha \models \beta$ if and only if $\alpha \wedge \neg \beta$ is unsatisfiable
• Proof by inference rules
  • Proof by applying inference rule to show alpha implies beta is valid
  • Rule 1 (Modus Ponens)
  • $\frac{\alpha \to \beta ,\alpha }{\beta }$
    • If you have the top in your knowledge base, the bottom can be derivevd
  • Rule 2 (And-Elimination)
    • $\frac{\alpha \wedge \beta }{\alpha }$
  • Rule 3 all logical equivalences can be used as inference rules
  • Monotonicity: set of entailed sentences can only increase as information is added to the KB

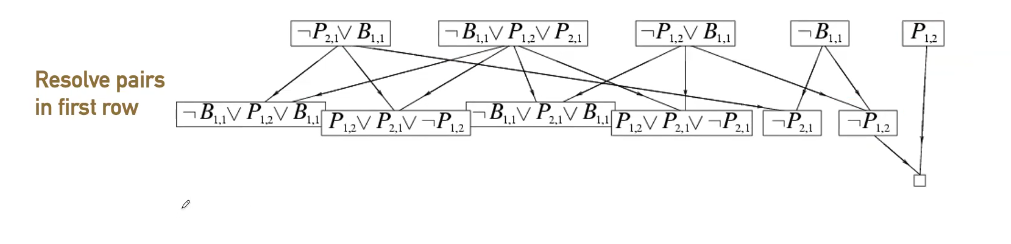
Proof by resolution §

• proof by showing ($KB\wedge \neg \alpha$) is unsatisfiable
• Sketch:
  • Negate the conclusion and add it to the knowledge base (add $\neg \alpha$ to KB)
  • Convert sentecnes in KB to conjunctive noirmal form (CNF)
  • Repeatedly apply the resolution inference rule until a contradiction is found
• Conversion to CNF
  • Every sentence in propositional logic is logically equivalent to a conjunction of clauses (which are disjunctions of literals)
    • Literal can be any symbol or its negation
    • CNF is an AND of literals OR’ed together
    • $(a\vee b\vee c)\wedge (d\vee e)$
    • Basically decompose it down to just OR, AND, and NOT. No parentheses except to separate the OR’ed together clauses (so no parentheses inside the clauses)
• Resolution inference rule for CNF
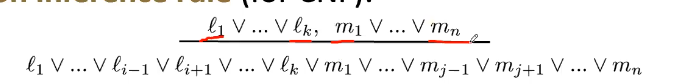  • Where $l_i$ and $m_j$ are complementary literals (i.e. one is the negation of the other)
  • We want to find an empty clause, find a contradiction
  • Resolution is sound and complete for propositional logic
  • 

Pros and Cons of Propositional Logic §

(Propositional Logic is basically what’s used in all the stuff above)

• Propositional logic is declarative
• Allows partial/disjunctive/negated information
• Is compositional: you can derive A and B from having both A and B
• Meaning in propositional logic is context-independent (unlike natural language where meaning depends on context)
• Propositional logic has limited expressive power (unlike natural language)
  • You cannot say “pits cause breezes in adjacent squares” except by writing a statement for EACH square and its adjacent squares
  • There ends up being a LOT of distinct proposition symbols and many many sentences

First-order Logic §

• Propositional logic assumes the world contains:
  • Facts - there is no breeze, it is snowing
• First order logic assumes the world contains:
  • Facts - there is no breeze, it is snowing
  • Objects - people, houses, numbers, colors
  • Relations - red, round, prime, brother of, bigger than, part of, comes between
  • Functions - father-of, best-friend, more-than, plus
• 
• 
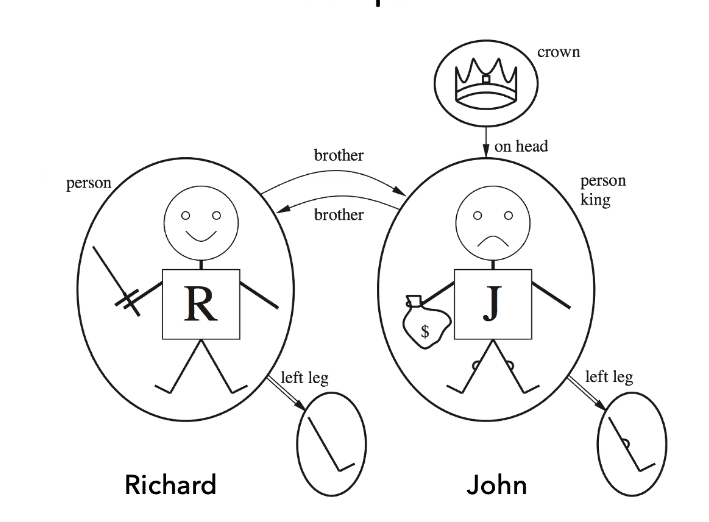
• Constants represent the objects
• Predicates represent relations between objects. They are sets of tuples of objects that are related.
• Functions are relations where a given set of objects are related to exactly one object
• Atomic sentences
  • Terms are constants, variables, or functions
  • Atomic sentences are predicates(terms) or term = term
• Complex sentences
  • Putting together atomic sentences using connectives
• Truth in first order logic
  • Model contains objects (domain elements) and realtions among them
  • Interpretation specifies referents for
    • Constant symobls -> objects
    • Predicate symbols -> relations
    • Function symbols -> functions
  • Sentences are true with respect to a model and an interpretation
    • An atomic sentence predicate(term 1, … term n) is true iff the objects referred to by term 1 through term n are in the RELATION referred to by the predicate
    • Intended interpretation - if you use the constant symbol John it refers to John, you don’t use Steve to refer to the object named John (cuz it’d be confusing)

Quantifiers §

• Universal quantification
  • $\forall <\text{variables},\text{sentence}>$
  • Typically implication is the main connective with $\forall$
  • Common mistake is using $\wedge$ as the main connective with $\forall$
    • $\forall xIN(x,CS471)\wedge Smart(x)$
    • Means “Everyone is in CS 471 and everyone is smart”
  • FOR ALL
• Existential quantification
  • $\exists <\text{variables}><\text{sentence}>$
  • Someone in CS471 is smart: $\exists xIN(x,CS471)\wedge Smart(x)$
  • THERE IS AT LEAST ONE
  • Common mistake is using implication as the main connective instead of $\wedge$
• Properties of quantifiers
  • ${\forall }_x{\forall }_y$ is the same as ${\forall }_y{\forall }_x$
  • ${\exists }_x{\exists }_y$ is the same as ${\exists }_y{\exists }_x$
  • ${\forall }_x{\exists }_y$ is NOT the same as ${\forall }_y{\exists }_x$
  • Quantifier duality: each can be expressed using the other
    • ${\forall }_{x}Likes(x,IceCream)$=== $\neg {\exists }_x\neg Likes(x,IceCream)$
    • “Every x likes ice cream” is same as “there does not exist a x who does not like ice cream”
• Examples
  • Sisters are siblings
  • ${\forall }_{x,y}Sister(x,y)\to Sister(y,x)$

Equality in FOL §

• term1 = term2 is true under a given interpretation if and only if term1 and term2 refer to the same object
• e.g. definition of sibling in terms of parent
• ${\forall }_{x,y}Sibling(x,y)\leftrightarrow [\neg (x=y)\wedge {\exists }_{m,f}\neg (m=f)\wedge Parent(m,x)\wedge Parent(f,x)\wedge Parent(m,y)\wedge Parent(m,x)]$