Probability

Uncertainty §

• General situation:
  • Observed variables (evidence): Agent knows certain things about the state of the world
  • Unobserved variables: Agent needs to reason about other aspects
  • Model: Agent knows something about how the known variables relate to the unknown variables Probabilistic Reasoning gives us a framework for managing our beliefs and knowledge

Probabilities §

• Probability Space ($\Omega ,F,P$)
• Sample space $\Omega$ Possible outcomes
• F = Events = a set of subsets of $\Omega$
  • An event is a subset of $\Omega$
• P = Probability measure on F
• P(A) = probability of event A
• $\Omega =\{1,2,3,4,5,6\}$
• Event A = Getting 1 = $\{1\}$
• $P(A)=P(\{1\})=\frac{1}{6}$

Random variables §

A random variable is a function that maps from $\Omega$ to some range (set of values it can take on)

• C = Head or Tail?
• T = is te temperature hot or cold
• D = the sum of two dice
• We denote random variables with capital letters
• Example random vairables have range:
  • C in {true, false}
  • T in {hot, cold}
  • D in {2, … 12}

Probability Distributions §

• A probability distribution is an assignment of weights to outcomes
• 
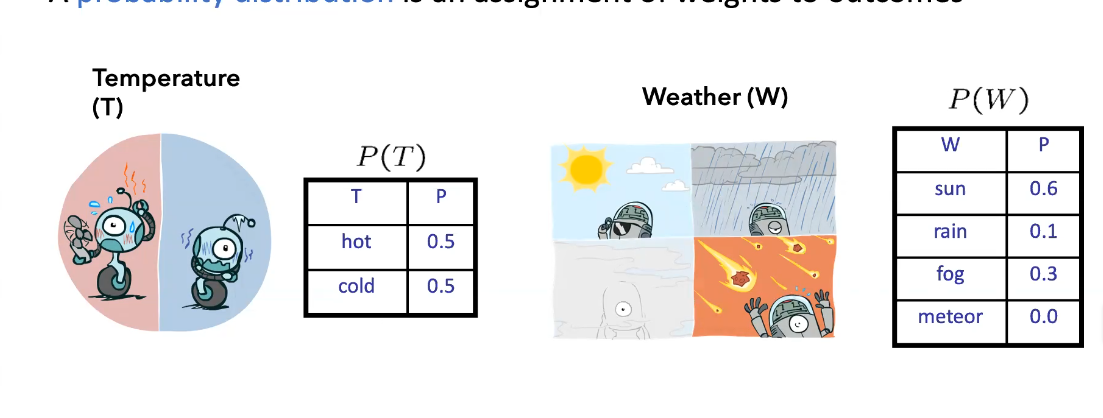
• $\forall xP(X=x)\ge 0$ and ${\sum }_{x}P(X=x)=1$
• The expected value of a random variable is the average, weighted by the probability distribution over outcomes
• Example: How long to get to the airport?
  • Time 65 min 75 min 90 min
  • P(T) 0.25 0.5 0.25
  • Multiply Time by its P(T) and add together, you get ~76.25 min

What are Probabilities? §

• Objectivist/frequentist answe:
  • Averages over repeated experiments (E.g. empirically estimating P(rain) from historical observation)
  • Assertion about how future experiments will go
  • New evidence changes the reference class
  • Makes one think of inherently random events, like rolling dice
• Subjectivist/Bayesian answer
  • What happens if its not something that’s not easily repetitive? i.e. Probability you are reading this right now
  • Degrees of belief about unobserved variables (e.g. an agents belief that its raining, given the temperature. Or Pacman’s belief that the ghost will turn left given the current state)
  • Often these probabilities are learnt from past experiences
  • New evidence updates your beliefs
• MOST machine learning and AI things take the Bayesian approach

Joint Distributions §

• A joint distribution over a set of random variables: $X_1,X_2,\dots ,X_n$
• Size of distribution for a set of $n$ variables with range sizes $d$?
  • For all but the smallest distributions its impractical to write out
• An events is a set $E$ of outcomes
• From a joint distribution, we can calculate the probability of any event

Marginal Distributions §

• Marginal distirbutions are sub-tables which eliminate variables
• Marginalization (summing out): Combine collapsed rows via addition
• $P(X_1=x_1)={\sum }_{x_2}P(X_1=x_1,X_2=x_2)$
• 
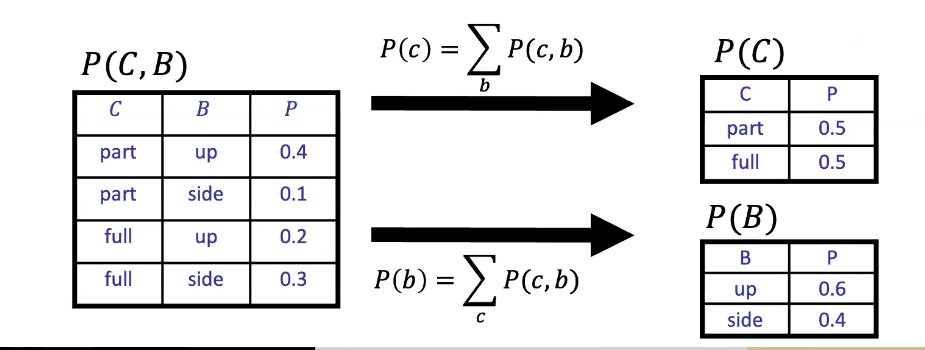
• These still are valid probability distributions and meet the requirements of being greater than or equal to 0 and adding up to 1

Conditional Probabilities §

A simple relation between joint and marginal probabilities

• The mathematical definition $P(a|b)=\frac{P(a,b)}{P(b)}$
• 
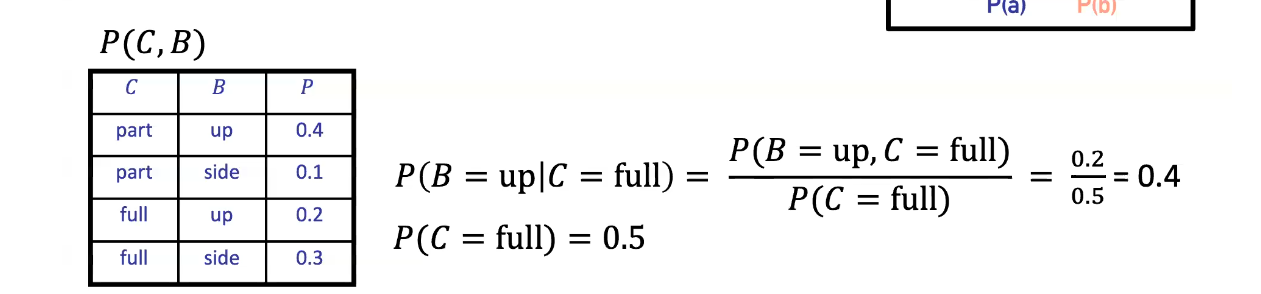
• Conditional distributions are probability distributions over some variables given fixed values of others
• 

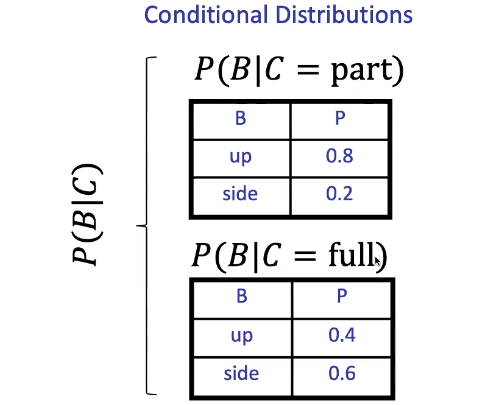
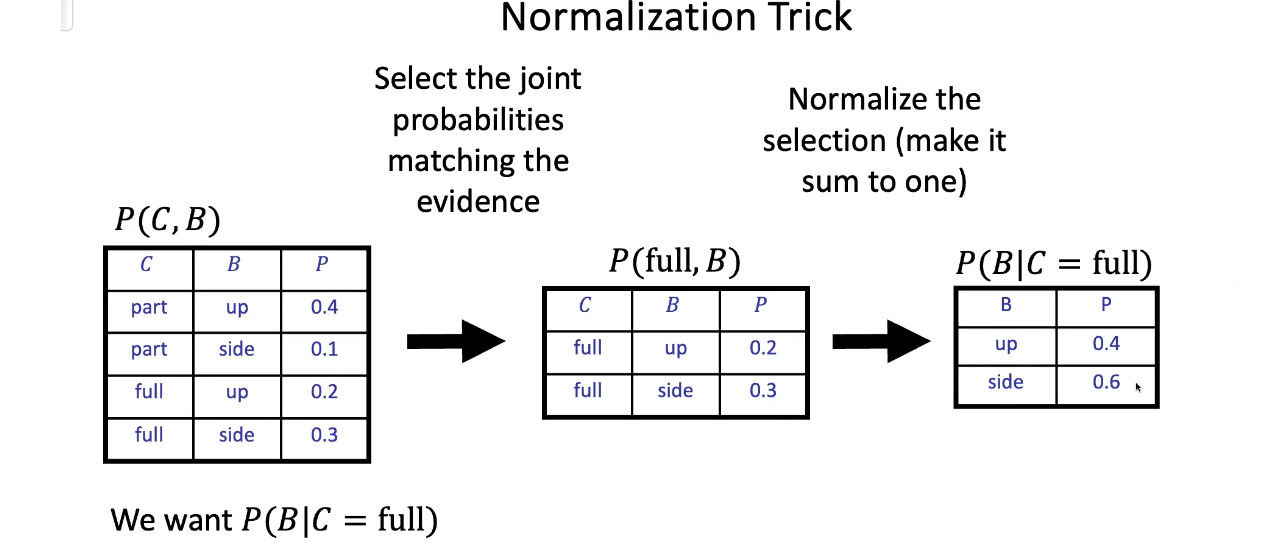
Normalization Trick §

We want P(B|C = full)

Independence §

Two variables are independent if:

• This says that their joint distribution factors into a product of two simpler distributions ${\forall }_{x,y}:P(x,y)=P(x)P(y)$
• Another form: ${\forall }_{x,y}:P(x|y)=P(x)$
• Independence is a simplifying modeling assumption
  • Empirical joint distributions at best are close to independent
  • What could we assume for { Weather, Traffic, Cavity, Toothache }?
    • Weather and Cavity are probably independent of each other
• Conditional Indpendence
  • Unconditional (absolute) indpendence is very rare
  • Conditionla independence is our most basic and robust form of knowledge about uncertain environments
  • X is conditionlly indepdenet of Y given Z
  • ${\forall }_{x,y,z}:P(x,y|z)=P(x|z)P(y|z)$
  • ${\forall }_{x,y,z}:P(x|z,y)=P(x|z)$
• The two types of indepdencene do not imply each other

Probabilistic Inference §

• Probabilistic inference: compute a desired probability form other known probabilities
• We generally compute conditional probabilities
  • P(on time | no reported accidents) = 0.9
  • These represent the agents beliefs given the evidence
• Observing new evidence causes beliefs to be updated
• Inference by Enumeration
  • General case:
    • Evidence variables: $E_1,\dots E_k=e_1\dots e_k$
    • Query $Q$
    • Hidden variables $H_1,\dots H_r$
    • We want $P(Q|e_1\dots e_k)$
  • Step 1 Select the entries consistent with the evidence
  • Step 2 sum out H to get joint of query and evidence
  • Step 3 normalize
• The Product Rule
  • Sometimes hve conditional distributions but we want the joint distribution
  • $P(y)P(x|y)=P(x,y)\leftrightarrow P(x|y)=\frac{P(x,y)}{P(y)}$
• The Chain Rule
  • More generally, can always write any joint distribution as an icnremental product of conditional distributions
  • $P(x_1,x_2,x_3)=P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)$
  • Basically a repeated application of the product rule
• Bayes’ Rule
  • Two ways to factor a joint distribution over two variables
  • $P(x,y)=P(x|y)P(y)=P(y|x)P(x)$
  • Dividing P(y) we get
  • $$$P(x|y) = \frac{P(y|x)}{P(y)} P(x)$$